Question

The set \[\left( {A \cup B \cup C} \right) \cap \left( {A \cap B' \cap C'} \right) \cap C'\] is equal to
A. \[B \cap C'\]
B. \[A \cap C\]
C. \[B' \cap C'\]
D. None of these

Answer 1

Hint: First we will first draw the Venn diagrams of the terms \[\left( {A \cup B \cup C} \right)\], \[\left( {A \cap B' \cap C'} \right)\] and \[C'\] of the given expression and then find the intersections from the three obtained diagrams to find the required value.

Complete step by step answer:

We are given that the set is \[\left( {A \cup B \cup C} \right) \cap \left( {A \cap B' \cap C'} \right) \cap C'\].

We will find the venn diagram of the \[\left( {A \cup B \cup C} \right)\], \[\left( {A \cap B' \cap C'} \right)\] and \[C'\] separately.

First, making the venn diagram of \[\left( {A \cup B \cup C} \right)\] by shading the all the sets A, B and C, we get

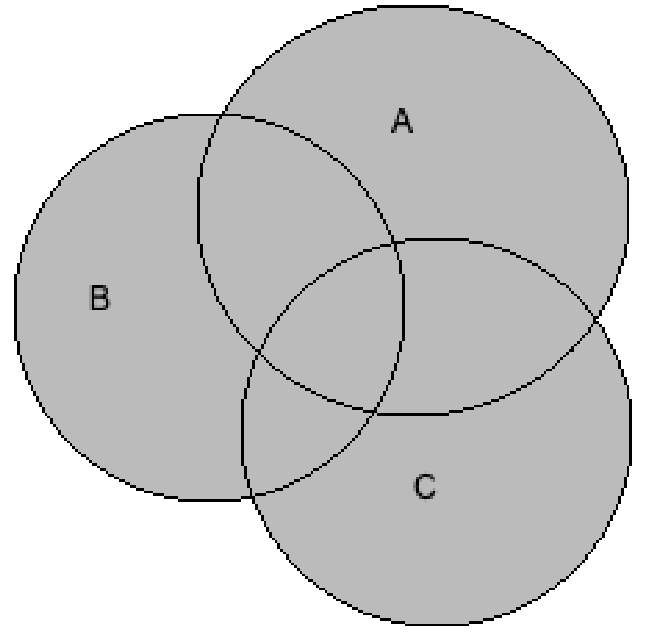
Making the Venn diagram of \[\left( {A \cap B' \cap C'} \right)\] by shading just the set for A, not B and not C, we get

Making the Venn diagram of \[C'\] by shading the complement of C, we get

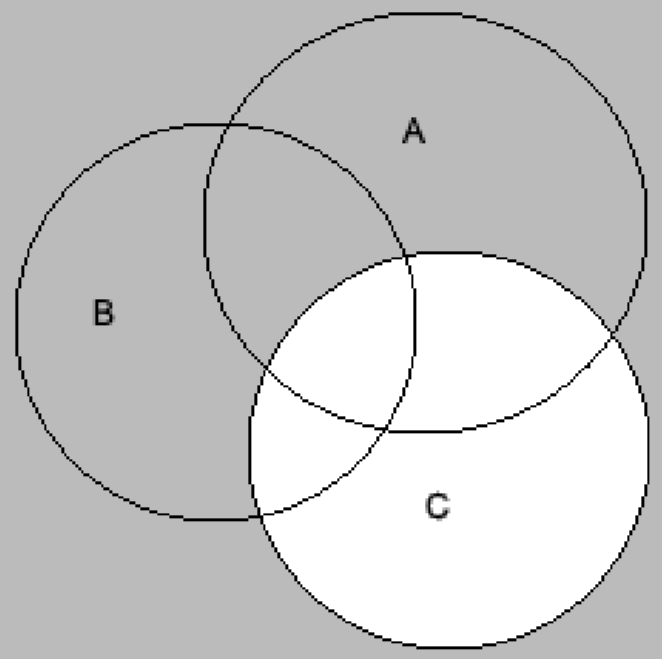
Now, finding the intersection of all the above three terms to find the value of \[\left( {A \cup B \cup C} \right) \cap \left( {A \cap B' \cap C'} \right) \cap C'\], we get

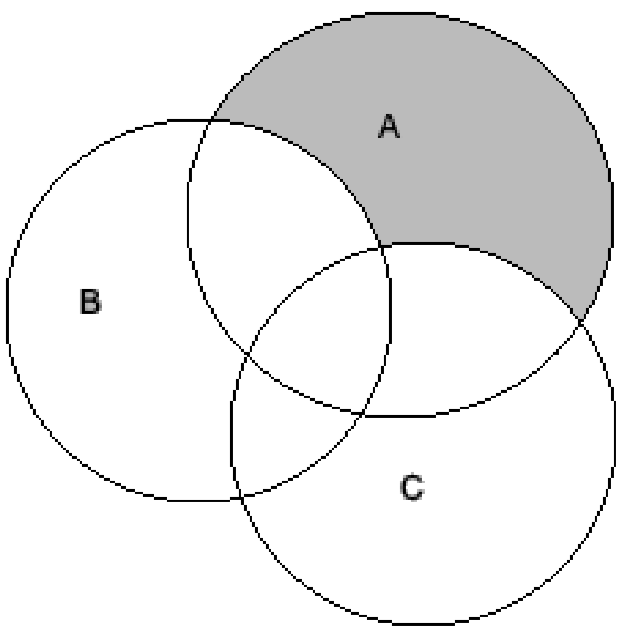
Thus, the required value from the above Venn diagram is \[A \cap B' \cap C'\].

Since none of the options match, option D is correct.

Note: In solving these types of questions, students should be familiar with the making of Venn diagrams, complements, union, and intersections. One should shade the region to be selected with some different colors for a better understanding. We should be careful whiles shading the region as one may shade a different part of the diagrams, which is wrong.