
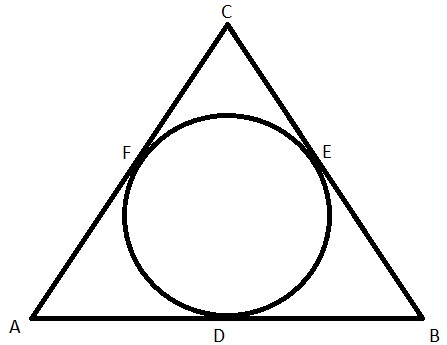
The semi perimeter of triangle ABC = 28 cm, then find the value of AF + BD + CE.
(a) 28 cm
(b) 16 cm
(c) 12 cm
(d) 19 cm

Answer
603.3k+ views
Hint: First, using the property of tangents from a point, find that AF = AD, DB = BE, and CF = CE. Then write the expression for the perimeter of triangle ABC as AB + BC + AC = 56 cm. Break AB, BC, and AC into (AD + BD), (BE + CE), and (AF + CF), respectively. Then, rearranging this and using the above found relations, we find the final answer.
Complete step-by-step answer:
In this question, we are given that the semi perimeter of triangle ABC = 28 cm.
We need to find the value of AF + BD + CE from the given figure.
We can see from the figure that the sides of the triangle are tangents to the circle.
We know a property of tangents on a circle that the length of tangents from an external point to a circle are equal.
Using this property, we will get the following:
AF = AD
DB = BE
CF = CE
Now, we are given that the semi perimeter of the triangle ABC is 28 cm.
We know that the perimeter of a triangle is double of the semi perimeter. Using this property, we will get the following:
Perimeter of triangle ABC = 56 cm
AB + BC + AC = 56 cm
(AD + BD) + (BE + CE) + (AF + CF) = 56 cm
(AD + AF) + (BD + BE) + (CE + CF) = 56 cm
2(AF + BD +CE) = 56 cm
AF + BD + CE = 28 cm
So, option (a) is correct.
Note: In this question, it is very important to realise that the sides of the triangle are tangents to the circle. Also, it is very important to know the relation between the semi perimeter and the perimeter and the property that length of tangents from an external point to a circle are equal.
Complete step-by-step answer:
In this question, we are given that the semi perimeter of triangle ABC = 28 cm.
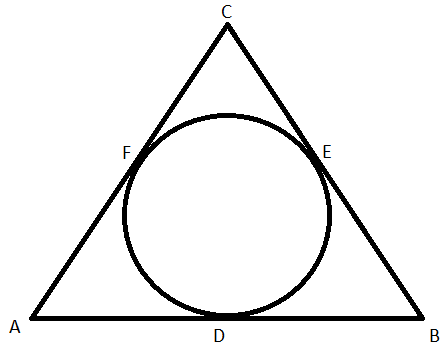
We need to find the value of AF + BD + CE from the given figure.

We can see from the figure that the sides of the triangle are tangents to the circle.
We know a property of tangents on a circle that the length of tangents from an external point to a circle are equal.
Using this property, we will get the following:
AF = AD
DB = BE
CF = CE
Now, we are given that the semi perimeter of the triangle ABC is 28 cm.
We know that the perimeter of a triangle is double of the semi perimeter. Using this property, we will get the following:
Perimeter of triangle ABC = 56 cm
AB + BC + AC = 56 cm
(AD + BD) + (BE + CE) + (AF + CF) = 56 cm
(AD + AF) + (BD + BE) + (CE + CF) = 56 cm
2(AF + BD +CE) = 56 cm
AF + BD + CE = 28 cm
So, option (a) is correct.
Note: In this question, it is very important to realise that the sides of the triangle are tangents to the circle. Also, it is very important to know the relation between the semi perimeter and the perimeter and the property that length of tangents from an external point to a circle are equal.
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
The shortest day of the year in India

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




