Question

The relation between edge length (a) and radius of atom (r) for BCC lattice is $\sqrt{3}a=4r$ .

Answer 1

Hint: The pre-knowledge of unit cells and crystal lattice will help us solve this problem. The relationship between atomic radius and the edge length of a unit cell can be derived for BCC structure to illustrate the given data.

Complete answer:
Let us learn about the crystal lattice and its types;
Crystal lattice- The arrangement of atoms or ions in the three-dimensional form in a crystal.
Unit cell- A unit cell is the smallest repeating unit of a crystal lattice.
Types of unit cell-
1. Simple cubic structure
2. Body centred cubic structure
3. Face centred cubic structure
Let us concentrate on the second type of a unit cell i.e. BCC structure;
-The BCC unit cell consists of the atoms at all the corners of the crystal and at the centre of the cube.
-Thus, 2 atoms are present in a BCC unit cell. As,
a. Corners of a cube- $8\times \frac{1}{8}=1$ atom.
b. Centre of a cube- 1 atom.
To analyse the relationship of edge length and radius for BCC crystal lattice; focus on the green coloured triangle in the diagram.

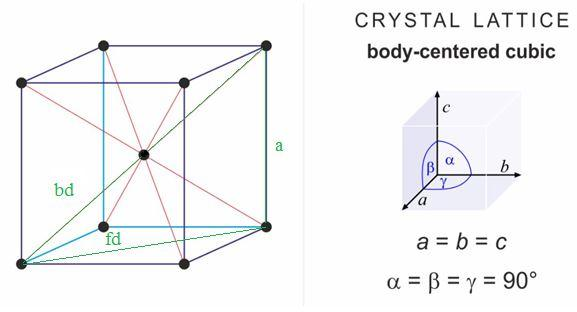
To find the relationship between the edge length of the cube and the radius of an atom, apply Pythagoras theorem to above given figure;
$\begin{align}
  & Sid{{e}_{1}}^{2}+Sid{{e}_{2}}^{2}=Hypoteneu{{s}^{2}} \\
 & f{{d}^{2}}+{{a}^{2}}=b{{d}^{2}} \\
 & b{{d}^{2}}={{a}^{2}}+{{a}^{2}}+{{a}^{2}} \\
 & b{{d}^{2}}=3{{a}^{2}} \\
\end{align}$
where,
a = side of a lattice
fd = face diagonal
bd = body diagonal = 4r
Thus,
$\begin{align}
  & {{\left( 4r \right)}^{2}}=3{{a}^{2}} \\
 & 4r=\sqrt{3}a \\
\end{align}$
where,
r = radius of atom

Note:
The relationship between the atomic radius and edge length is different for all types of unit cells; each one has its own significance.
Also, the packing efficiency can be calculated for each type of crystal lattice when we know this relationship.