Question

The refractive indices of flint glass prisms for $C,D$ and $F$ lines are $1.790,1.795$ and $1.805$ respectively. The dispersive power of the flint glass prism is
$\begin{align}
  & A)0.141 \\
 & B)0.125 \\
 & C)0.018 \\
 & D)0.929 \\
\end{align}$

Answer 1

Hint: Dispersive power of a prism is defined as the ratio of angular dispersion to the angle of deviation for the mean wavelength. $C,D$ and $F$ lines of a prism correspond to red, yellow and violet lines of the prism. Angle of deviation of a particular color of light when passed through a prism is dependent on the refractive index of that particular color of light.

Formula used:
$\omega =\dfrac{{{\delta }_{v}}-{{\delta }_{r}}}{{{\delta }_{y}}}=\dfrac{{{\mu }_{v}}-{{\mu }_{r}}}{{{\mu }_{y}}-1}$

Complete step by step answer:
Dispersive power of the material of a prism refers to the ratio of angular dispersion to the angle of deviation for the mean wavelength. Here, angle of deviation for the mean wavelength corresponds to the yellow line of the prism. $C,D$ and $F$ lines of a prism correspond to red, yellow and violet lines of the prism. Mathematically, dispersive power of a prism is given by
$\omega =\dfrac{{{\delta }_{v}}-{{\delta }_{r}}}{{{\delta }_{y}}}$
where
$\omega $ is the dispersive power of a prism
${{\delta }_{v}}$ is the angle of deviation of violet light
${{\delta }_{r}}$ is the angle of deviation of red light
${{\delta }_{y}}$ is the angle of deviation of yellow light (mean wavelength)
${{\delta }_{v}}-{{\delta }_{r}}$ refers to the angular dispersion of the prism
Let this be equation 1.
The figure given below can be referred for clarity.

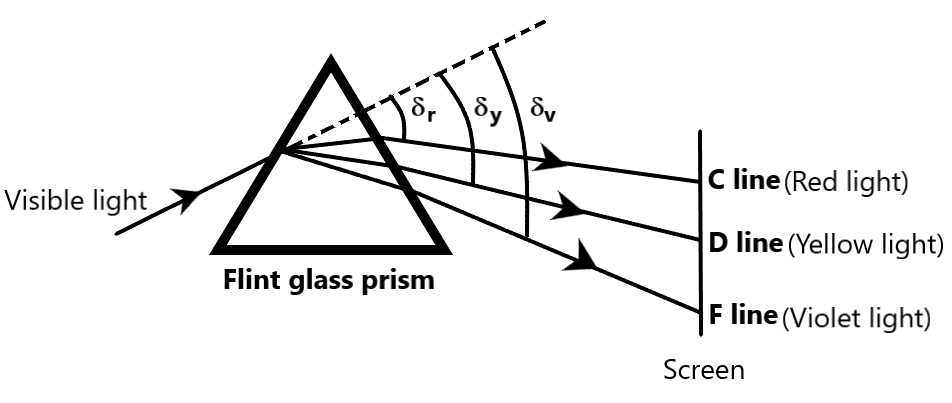
Since angular dispersion and angle of deviation for the mean wavelength are related to the respective refractive indices of red, yellow and violet lines of the prism, dispersive power of the prism is also related to the refractive indices of the mentioned. Therefore, equation 1 can be rewritten as
$\omega =\dfrac{{{\delta }_{v}}-{{\delta }_{r}}}{{{\delta }_{y}}}=\dfrac{{{\mu }_{v}}-{{\mu }_{r}}}{{{\mu }_{y}}-1}$
where
${{\mu }_{v}}$ is the refractive index corresponding to violet light or $F$ line
${{\mu }_{r}}$ is the refractive index corresponding to red light or $C$ line
${{\mu }_{y}}$ is the refractive index corresponding to yellow light or $D$ line
Let this be equation 2.
Coming to our question, we are provided with a flint glass prism. It is also given that
${{\mu }_{r}}=1.790$, is the refractive index corresponding to $C$ line of the flint glass prism
${{\mu }_{v}}=1.805$, is the refractive index corresponding to $F$ line of the prism
${{\mu }_{y}}=1.795$, is the refractive index corresponding to $D$ line of the prism
Substituting these values in equation 2, we have
$\omega =\dfrac{{{\mu }_{v}}-{{\mu }_{r}}}{{{\mu }_{y}}-1}=\dfrac{1.805-1.790}{1.795-1}=\dfrac{0.015}{0.795}=0.018{}^\circ $
Therefore, dispersive power of the given flint glass prism is equal to $0.018{}^\circ $. The correct answer is option $C$.

Note:
The question can also be approached in a different way, using the formula given below:
\[\omega =\dfrac{{{\mu }_{F}}-{{\mu }_{C}}}{{{\mu }_{D}}-1}\]
where
${{\mu }_{F}}$ is the refractive index corresponding to $F$ line
${{\mu }_{C}}$ is the refractive index corresponding to $C$ line
${{\mu }_{D}}$ is the refractive index corresponding to $D$ line
This can be considered as a direct approach to the question and students need not think about red, yellow and violet lines, here.