Question

What will be the ratio of speed in the first two seconds to the next four seconds?

(A)$\sqrt 2 :1$
(B)$3:1$
(C) $2:1$
(D)$1:2$

Answer 1

Hint: This is a graph between distance and time. The slope of this graph can be used to determine speed. The speed in a particular interval of time can be obtained by calculating the slope in that region of the graph. The slope of a graph of the x-axis vs y-axis has to be known.
Formula used:
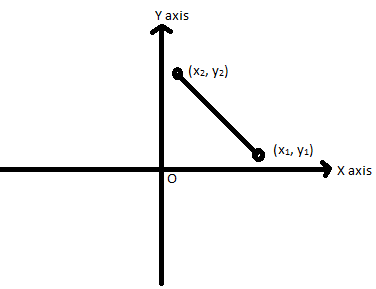
The slope of a graph, in general, can be given as:-
$slope = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$

Complete step by step answer:
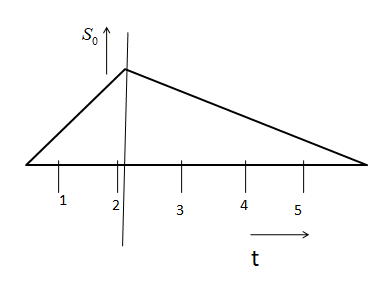
The graph will be

The formula of the slope is $slope = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
The graph given in the problem is

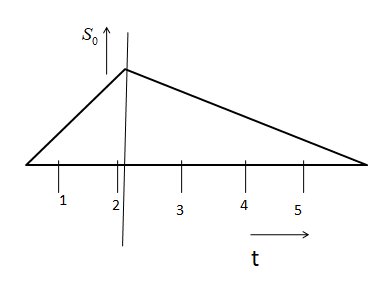
It is shown in the distance-time graph.
The speed is calculated by evaluating the slope.
 Let speed in the first two seconds is \[{v_1}\] .
\[{{\text{v}}_1} = \dfrac{{S - 0}}{{2 - 0}} = \dfrac{S}{2}\] ….. (i) (since \[{y_1} = 0\] and \[{y_2} = S\] (distance) and X axis is representing time)
And, speed in the next four seconds is \[{v_2}\] .
\[ \Rightarrow {v_2} = \dfrac{{S - 0}}{{6 - 2}} = \dfrac{{\text{S}}}{4}\] …… (ii) (since \[{y_1} = 0\] and \[{y_2} = S\] (distance) and X axis is representing time)
From the ratio of \[{v_1}\] and \[{v_2}\] we will get
\[\dfrac{{{v_1}}}{{{v_2}}} = \dfrac{{\dfrac{S}{2}}}{{\dfrac{S}{4}}} = \dfrac{2}{1}\]
Therefore, the required ratio is \[2:1\]

Hence, the correct option is (C) .

Note:
Speed is defined by the rate of the total distance covered by an object. It is a scalar quantity. When an object travels its $1st$ half journey with some distance and time that is different from the remaining journey, then the average speed is required. The average speed can be calculated by the ratio of the total distance to the total time of the journey. In the graph of distance vs time, the slope determines the speed.