Question

The ratio in which \[i + 2j + 3k\] divides the join of \[ - 2i + 3j + 5k\] and \[7i - k\] is?
A.\[ - 3:2\]
B.\[1:2\]
C.\[2:3\]
D.\[ - 4:3\]

Answer 1

Hint: First we will first assume that \[m\] is the ratio in which \[i + 2j + 3k\] divides the join of \[ - 2i + 3j + 5k\] and \[7i - k\]. Then we will find the coordinates for the given equations and then we will simplify the equation \[\dfrac{{7m - 2}}{{m + 1}} = 1\] to find the required value.

Complete step-by-step answer:
Let us assume that \[m\] is the ratio in which \[i + 2j + 3k\] divides the join of \[ - 2i + 3j + 5k\] and \[7i - k\].
We are given that the \[i + 2j + 3k\] divides the join of \[ - 2i + 3j + 5k\] and \[7i - k\].
We will first find the coordinates for the given equations, \[i + 2j + 3k\], \[ - 2i + 3j + 5k\] and \[7i - k\].
We have,
\[\left( {1,2,3} \right)\]
\[\left( { - 2,3,5} \right)\]
\[\left( {7,0, - 1} \right)\]
Plotting the above points on the line, we get

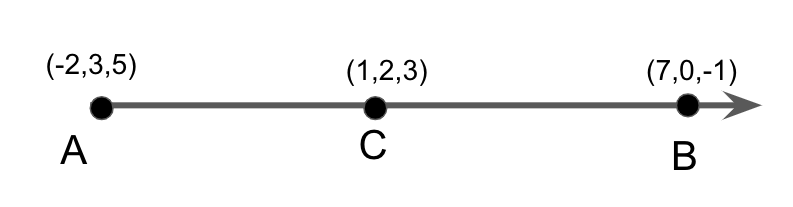
Now equating the three points A, B and C, we get
\[ \Rightarrow \dfrac{{7m - 2}}{{m + 1}} = 1\]
Cross-multiplying the above equation, we get
\[ \Rightarrow 7m - 2 = m + 1\]
Subtracting the above equation by \[m\] on both sides, we get
\[
   \Rightarrow 7m - 2 - m = m + 1 - m \\
   \Rightarrow 6m - 2 = 1 \\
 \]
Adding the above equation by 2 on both sides, we get
\[
   \Rightarrow 6m - 2 + 2 = 1 + 2 \\
   \Rightarrow 6m = 3 \\
 \]
Dividing the above equation by 6 on both sides, we get
\[
   \Rightarrow \dfrac{{6m}}{6} = \dfrac{3}{6} \\
   \Rightarrow m = \dfrac{1}{2} \\
 \]
Hence, the required ratio is \[1:2\].
Thus, option B is correct.

Note: In solving these types of questions, students should make diagrams for better understanding and label the vertices properly to avoid confusion. One should know that the ratio is a way how much of one thing there is compared to another thing.