Question

The radius of the incircle of a triangle is 4cm, and the segments into which one side is divided by the point of contact are 6cm and 8cm. Determine the sum of the other two sides of the triangle.

Answer 1

Hint: Use the fact that the inradius of a circle is given by $r=\dfrac{\Delta }{s}$, where $\Delta $ is the area of the triangle and is the semi perimeter of the triangle. Use the fact the area of the triangle is given by the Heron’s formula as $\Delta =\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-v \right)}$, where the symbols have their usual meaning. Join ID and AD and hence prove that $AD=ID\cot \dfrac{A}{2}$. Use the fact that in triangle ABC $\cot \dfrac{A}{2}=\sqrt{\dfrac{s\left( s-a \right)}{\left( s-b \right)\left( s-c \right)}}$. Hence prove that AD = s-a and DC = s-c. Using the fact that b = AD+DC = 14, prove that a=2+c and hence prove that s = 8+c.

Complete step-by-step solution
Now, using the fact that $r=\dfrac{\Delta }{s}=\sqrt{\dfrac{\left( s-a \right)\left( s-b \right)\left( s-c \right)}{s}}$ form an equation in c. Solve for c. Hence find the value of a and c. Hence find the sum of the other two sides.

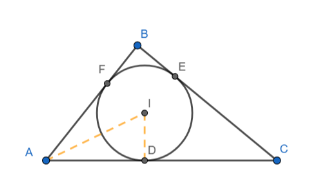
Given: A triangle ABC. The incircle of the triangle ABC meets AC at D, BC at E and AB at F. I is the incentre of the triangle ABC. ID = 4, AD = 6 and DC = 8.
To determine: AB+AC, i.e. a+c.
Construction: Join IA and ID.
In triangle IAD, we have
$\cot \dfrac{A}{2}=\dfrac{AD}{ID}$
Multiplying both sides by ID, we get
$AD=ID\cot \dfrac{A}{2}$
We know that in triangle ABC $\cot \dfrac{A}{2}=\sqrt{\dfrac{s\left( s-a \right)}{\left( s-b \right)\left( s-c \right)}}$
Hence, we have
$AD=r\sqrt{\dfrac{s\left( s-a \right)}{\left( s-b \right)\left( s-c \right)}}$
We know that in triangle ABC, $r=\dfrac{\Delta }{s}$ and from Heron’s formula, we have $\Delta =\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$
Hence, we have
$r=\dfrac{\sqrt{\left( s \right)\left( s-a \right)\left( s-b \right)\left( s-c \right)}}{s}=\sqrt{\dfrac{\left( s-a \right)\left( s-b \right)\left( s-c \right)}{s}}$
Hence, we have
$AD=\sqrt{\dfrac{\left( s-a \right)\left( s-b \right)\left( s-c \right)}{s}}\times \sqrt{\dfrac{s\left( s-a \right)}{\left( s-b \right)\left( s-c \right)}}=s-a$
Hence, we have s-a = 6
Multiplying both sides by 2, we get
2s-2a = 12
We know that 2s = a+b+c
Hence, we have
a+b+c -2a = 12
i.e. b+c-a = 12
Now, we have b = AD+DC = 6+8 = 14
Hence, we have
c-a+14 = 12
Subtracting 12 from both sides, we get
c-a+2 = 0
Adding a on both sides, we get
a=2+c (i)
Hence, we have
$s=\dfrac{a+b+c}{2}=\dfrac{2+c+14+c}{2}=8+c$
Now, we know that
$r=\sqrt{\dfrac{\left( s-a \right)\left( s-b \right)\left( s-c \right)}{s}}$
Hence, we have
$\begin{align}
  & 4=\sqrt{\dfrac{\left( 8+c-2-c \right)\left( 8+c-14 \right)\left( 8+c-c \right)}{8+c}} \\
 & \Rightarrow 4=\sqrt{\dfrac{6\left( c-6 \right)8}{8+c}} \\
\end{align}$
Squaring both sides, we get
$16=\dfrac{48}{8+c}\left( c-6 \right)$
Dividing both sides by 16, we get
$1=\dfrac{3\left( c-6 \right)}{c+8}$
Multiplying both sides by c+8, we get
c+8 = 3c-18
Subtracting c from both sides, we get
2c -18 = 8
Adding 18 on both sides, we get
2c = 26
Dividing by 2 on both sides, we get
c=13
Substituting the value of c in equation (i), we get
a =13+2 = 15
Hence the sum of the other two sides is equal to a+c = 13+15 = 28.

Note: Verification:
We have a = 15, b = 14 and c = 13
Hence, we have $s=\dfrac{15+14+13}{2}=21$
Hence, we have
$\Delta =\sqrt{21\left( 21-15 \right)\left( 21-14 \right)\left( 21-13 \right)}=\sqrt{21\times 6\times 7\times 8}=84$
Hence, we have $r=\dfrac{\Delta }{s}=\dfrac{84}{21}=4$
Also, we have AD = s-a = 21-15 = 6 and DC = s-c = 21-13 = 8
Hence our answer is verified to be correct.