Question

The radius of the curvature of the convex surface of a Plano-convex lens is 20 cm. If the refractive index of the material of the lens is 1.5. Then what is the focal length of the Plano- convex lens?
A. 10 cm
B. 20 cm
C. 30 cm
D. 40 cm

Answer 1

Hint: Here, we will proceed by directly applying the formula for the focal length of the Plano convex lens. We are given the radius of the curvature of the convex surface and the refractive index of the material of the lens with which we can easily find out the focal length of the Plano-Convex lens.

Formula used: $\dfrac{1}{f} = (\dfrac{{{\mu _2}}}{{{\mu _1}}} - 1)(\dfrac{1}{{R_1}} - \dfrac{1}{{R_2}})$

Complete Step-by-Step solution:

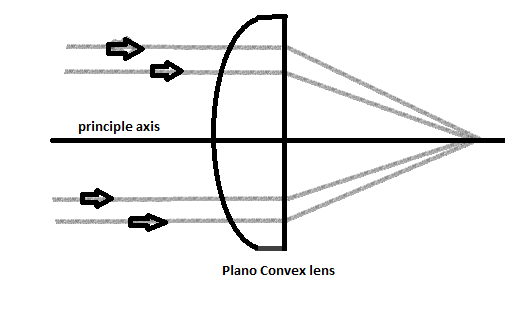
The radius of the curvature of the convex surface of a Plano-convex lens is given as 20 cm.
The refractive index of the material of the lens is 1.5
The focal length of the Plano convex lens can be calculated by the formula
$\dfrac{1}{f} = (\dfrac{{{\mu _2}}}{{{\mu _1}}} - 1)(\dfrac{1}{{R_1}} - \dfrac{1}{{R_2}})$
Here, f is the focal length of the Plano-convex lens.
${\mu _2}$ is the refractive index of the material of the lens.
${\mu _1}$ is the refractive index of the surrounding.
$R_1$ is the Radius of the curvature of the side on which the incident ray falls.
$R_2$ is the Radius of the curvature of the other side of the lens.
Here in this question, there is no other material given so we will take air as surrounding. The refractive index of the air is 1.
Also, the radius of the curvature of the plane mirror is infinity. So, the radius of the curvature of the plane side of the lens is infinity.
By assigning all the values in the formula, we will get the focal length of the Plano-convex lens
$
  \therefore \dfrac{1}{f} = (\dfrac{{1.5}}{1} - 1)(\dfrac{1}{{20}} - \dfrac{1}{\infty }) \\
   \Rightarrow \dfrac{1}{f} = (\dfrac{1}{2})(\dfrac{1}{{20}} - 0) \\
   \Rightarrow \dfrac{1}{f} = \dfrac{1}{{40}} \\
   \Rightarrow f = 40{\text{ cm}} \\
$
$\therefore {\text{ Option D is the correct answer}}$

Note- In differential geometry, the radius of curvature, R is the reciprocal of the curvature. For a curve, it equals the radius of the circular arc which best approximates the curve at that point. For surfaces, the radius of curvature is the radius of a circle that best fits a normal section.