Question

The radii of the two columns in a $U$ tube are ${r_1}$ and ${r_2}$, when a liquid of density (angle of contact is \[{0^o}\]) is filled in it, the level difference of the liquid in the two arms in $h$. The surface tension of the liquid is: ($g = $acceleration due to gravity).
(A) $\dfrac{{\rho gh{r_1}{r_2}}}{{2({r_2} - {r_1})}}$
(B) $\dfrac{{\rho gh({r_2} - {r_1})}}{{2{r_2}{r_1}}}$
(C) \[\dfrac{{2({r_1} - {r_2})}}{{\rho gh{r_2}{r_1}}}\]
(D) \[\dfrac{{2({r_1} - {r_2})}}{{\rho gh}}\]

Answer 1

Hint: Surface tension is nothing but the ability of liquid surfaces to shrink into minimum surface area. This property of a liquid allows it to block an external force as its molecules have cohesive nature.

Formula used:
The rise of liquid in the capillary tube can be calculated using the formula $h = \dfrac{{2T}}{{r\rho g}}$.

Complete step by step answer:
The cohesive nature of the liquid molecules is responsible for resisting an external force and shrinking into the minimum surface possible. This phenomenon is called as surface tension.

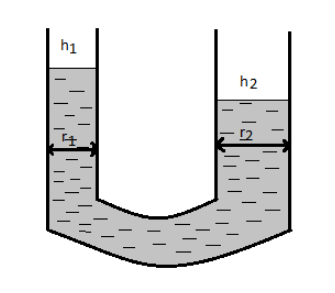
Let ${h_1}$ be the height in the tube having radius ${r_1}$.
So, we have ${h_1} = \dfrac{{2T}}{{{r_1}\rho g}} - - - - - (1)$
Similarly, let ${h_2}$ be the height in the tube having radius ${r_2}$.
So, we have ${h_2} = \dfrac{{2T}}{{{r_2}\rho g}} - - - - - (2)$
The level difference of liquid in the two arms can be given by
$h = {h_1} - {h_2}$
After substituting values from equations $(1)$ and $(2)$, we get
\[
h = \dfrac{{2T}}{{{r_1}\rho g}} - \dfrac{{2T}}{{{r_2}\rho g}} \\
\Rightarrow h = \dfrac{{2T}}{{\rho g}}[\dfrac{1}{{{r_1}}} - \dfrac{1}{{{r_2}}}] \\
\therefore h = \dfrac{{2T}}{{\rho g}}[\dfrac{{{r_2} - {r_1}}}{{{r_1}{r_2}}}] \\
\]
After rearranging the terms, we get $T = \dfrac{{h\rho g{r_1}{r_2}}}{{2({r_2} - {r_1})}}$
Thus, we can conclude that the surface tension of the liquid is $\dfrac{{\rho gh{r_1}{r_2}}}{{2({r_2} - {r_1})}}$.

So, option A is the correct answer.


Note: In this example, the height $h$ was mentioned, so we used the formula $h = \dfrac{{2T}}{{r\rho g}}$. For other examples, force and length can also be used to find out the surface tension by using the formula, $T = \dfrac{1}{2} \times \dfrac{F}{L}$where $T$ is the surface tension, $F$ is the force, and $L$ is the length.