Question

The radii of the bases of two right circular solid cones of same height are ${r_1}{\text{ and }}{r_2}$ respectively. The cones are melted and recast into a solid sphere of radius R . Show that the height of each cone is given by $h = \dfrac{{4{R^3}}}{{{r_1}^2 + {r_2}^2}}$ .

Answer 1

Hint- To solve this particular type of question we need to express the volumes of both solid cones with radii ${r_1}{\text{ and }}{r_2}$ respectively. Add the volumes and equate it with the volume of casted solid sphere , after cancelling the common terms find the value of h .

Complete step-by-step solution -

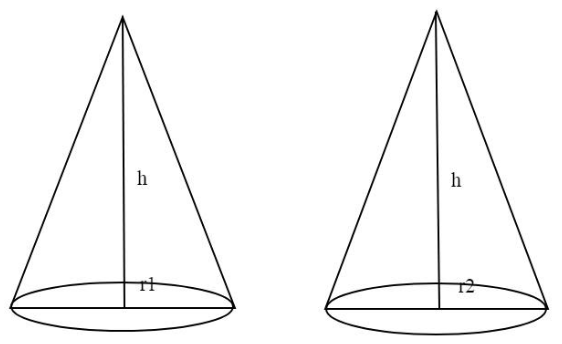
${V_1}$ be the volume of first cone with radius = ${r_1}$
${V_2}$ be the volume of second cone with radius = ${r_2}$
${V_1} = \dfrac{1}{3}\pi {r_1}^2h$
${V_2} = \dfrac{1}{3}\pi {r_2}^2h$
Now the volume of the new sphere will equal to the sum of the volumes of both cones .
Volume of the sphere = $\dfrac{4}{3}\pi {R^3}$
Therefore ,
$\begin{gathered}
  \dfrac{4}{3}\pi {R^3} = \dfrac{1}{3}\pi {r_1}^2h + \dfrac{1}{3}\pi {r_1}^2h \\
   \Rightarrow 4{R^3} = {r_1}^2h + {r_1}^2h \\
   \Rightarrow 4{R^3} = h\left( {{r_1}^2 + {r_1}^2} \right) \\
    \\
\end{gathered} $
$ \Rightarrow h = \dfrac{{4{R^3}}}{{\left( {{r_1}^2 + {r_2}^2} \right)}}$

Note – Remember to recall the formula of volume of a cone and a sphere to solve such type of questions . It is important to know that if two solids are melted and recast into another solid then the sum of the volumes of both solids is equal to the recast solid . Thus unlike the surface areas , the volume is the only quantity that doesn't change .