Question

The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rectangle, if:
A. PQRS is a rectangle
B. PQRS is a parallelogram
C. Diagonals of PQRS are perpendicular
D. Diagonals of PQRS are equal

Answer 1

Hint: First, we shall analyze the given information so that we are able to solve this problem. Here, we are given two quadrilaterals. We are given a quadrilateral PQRS. Let A be the mid-point of the side PQ, B be the mid-point of the side QR, C is the mid-point of the side SR and D be the mid-point of the side PS.
Hence, the quadrilateral ABCD is formed by joining the mid-points of the sides of the quadrilateral and ABCD is a rectangle.

Complete step by step answer:
  We are given a quadrilateral PQRS.
Let A be the mid-point of the side PQ, B be the mid-point of the side QR, C is the mid-point of the side SR and D be the mid-point of the side PS.
Hence, the quadrilateral ABCD is formed by joining the mid-points of the sides of the quadrilateral and ABCD is a rectangle.
A diagram is given below for the above descriptions.

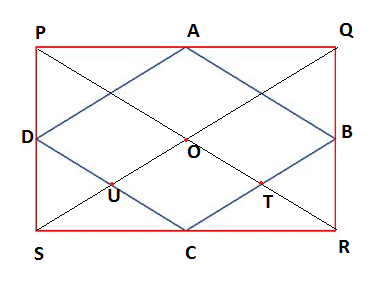
In $\vartriangle QSR$ , B is the mid-point of QR and C is the mid-point of SR.
Since BC is the line segment joining the sides QR and SR, using the mid-point theorem we have
$BC = \dfrac{1}{2}SQ$
Also, we have\[BC\parallel SQ\]
Hence, \[UO\parallel CT\] …….$\left( 1 \right)$
In$\vartriangle PSR$ , C is the mid-point of SR and D is the mid-point of PS.
Since CD is the line segment joining the sides SR and PS, using the mid-point theorem we have
$CD = \dfrac{1}{2}PR$
Also, we have\[CD\parallel PR\]
Hence, \[UC\parallel OT\] …….$\left( 2 \right)$
From $\left( 1 \right)$and$\left( 2 \right)$, we have rectangle UOTC is a parallelogram
Since ABCD is a rectangle, $\angle C = {90^\circ }$.
Also from the definition of a parallelogram, we have $\angle C = \angle O = {90^\circ }$
Since$\angle O = {90^\circ }$we can easily say that $PR \bot QS$(We all know that the diagonals of a rhombus are perpendicular to each other)
Hence, the diagonals of PQRS are perpendicular.

So, the correct answer is “Option C”.

Note: The mid-point theorem states that whenever the line segment that joins the mid-points of any two sides of a triangle is parallel to the third side and it is equal to half of the third side.
For example, if DE is the line segment joining the side AB and AC is parallel to BC.
Also, $DE = \dfrac{1}{2}BC$