Question

The quadratic polynomial having zeros are 1 and -2 is.
(a) ${{x}^{2}}-x-2$
(b) ${{x}^{2}}-x+2$
(c) ${{x}^{2}}+x-2$
(d) ${{x}^{2}}+x+2$

Answer 1

Hint: For solving this question we will simply find the sum and the product of the given roots and substitute their values in the formula ${{x}^{2}}-\left( \text{sum of the roots} \right)x+\left( \text{product of the roots} \right)$ to get the required quadratic polynomial. After that, we will see the plot of the polynomial and verify our answer.

Complete step-by-step solution -
Given:
We have to find the quadratic polynomial having roots 1 and -2.
Now, before we proceed we should know that if $x=\alpha $ and $x=\beta $ are roots of a quadratic polynomial $\left( x-\alpha \right)\left( x-\beta \right)={{x}^{2}}-\left( \alpha +\beta \right)x+\alpha \beta $ and we can write it as ${{x}^{2}}-\left( \text{sum of the roots} \right)x+\left( \text{product of the roots} \right)$ .
Now, we come back to our question in which we have to find the quadratic polynomial having roots 1 and 2. And from the above discussion, we can say that the required polynomial will be $\left( x-\alpha \right)\left( x-\beta \right)={{x}^{2}}-\left( \alpha +\beta \right)x+\alpha \beta $ with the value of $\alpha =1$ and $\beta =-2$ . Then,
$\begin{align}
  & \left( x-\alpha \right)\left( x-\beta \right)={{x}^{2}}-\left( \alpha +\beta \right)x+\alpha \beta \\
 & \Rightarrow \left( x-1 \right)\left( x+2 \right)={{x}^{2}}-\left( 1-2 \right)x-2 \\
 & \Rightarrow \left( x-1 \right)\left( x+2 \right)={{x}^{2}}+x-2 \\
\end{align}$
Now, from the above result, we conclude that the quadratic polynomial having zeros 1 and -2 will be ${{x}^{2}}+x-2$ . For better clarity look at the figure below:

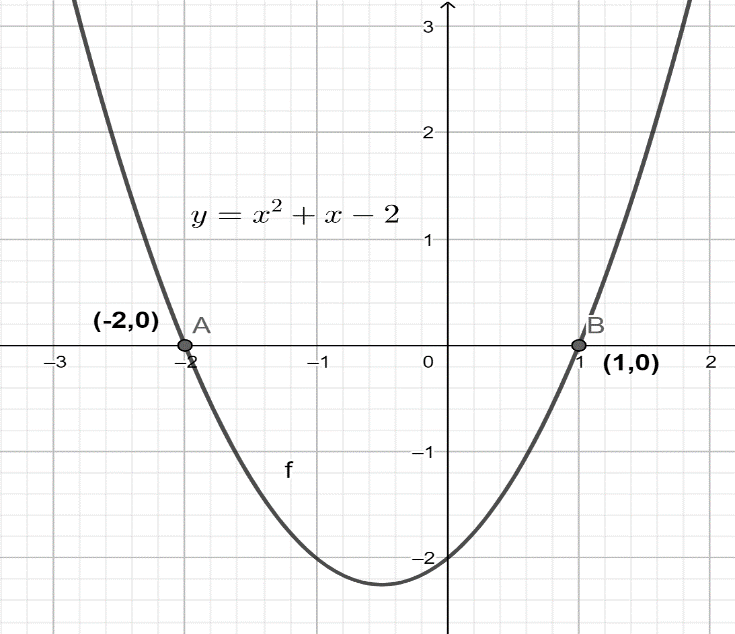
In the above figure, the curve $y={{x}^{2}}+x-2$ intersects the x-axis at two points A (-2,0) and B (1,0) and it is evident that ${{x}^{2}}+x-2$ is the quadratic polynomial having zeros 1 and -2.
Thus, ${{x}^{2}}+x-2$ is the required quadratic polynomial.
Hence, option (c) will be the correct option.

Note: Here, the student should first understand what is asked in the question and then proceed in the right direction to get the correct answer quickly. Moreover, though the problem is very easy, but we should write the expression of the required polynomial without any mistake and in the end, we should verify our answer with a graph and strengthen our basic concepts.