Question

The polar equation of the line passing through \[\left( {4,\dfrac{{2\pi }}{2}} \right)\] and perpendicular to the line joining origin to this point is

Answer 1

Hint: We will locate the point on the graph. We will sketch the required line according to the conditions given in the question. We will convert the equation of the line into the polar form using the formulas for converting rectangular coordinates to polar coordinates.
Formulas used:
 We will use following formulas for converting rectangular coordinates to polar coordinates:
\[x = r\cos \theta \]
\[y = r\sin \theta \]
\[\sqrt {{x^2} + {y^2}} = r\]

Complete step-by-step answer:
The point \[\left( {4,\dfrac{{2\pi }}{2}} \right)\] is equivalent to the point \[\left( {4,\pi } \right)\]. The modulus of the point represented by \[\left( {4,\dfrac{{2\pi }}{2}} \right)\] is 4 and it makes an angle of \[\pi \] radians with the positive \[x\] - axis. We will locate this point on the graph:

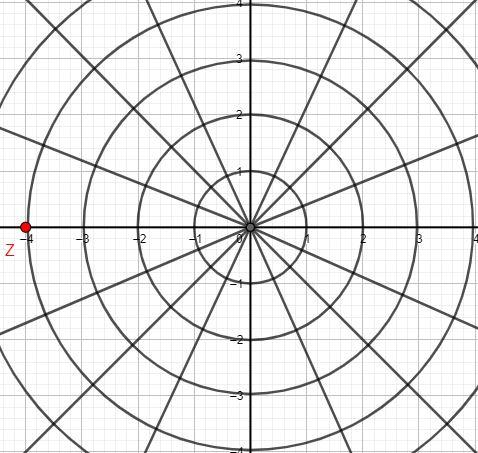
The point Z in red colour represents the required point. The point Z has value \[\left( {4,\pi } \right)\] in polar coordinates and value \[\left( { - 4,0} \right)\] in rectangular coordinates.
We can see from the figure that the line that is joining the point to the origin is the \[x\] - axis. We need a line that is perpendicular to the line joining the origin to this point i.e. our line will be perpendicular to the \[x\] - axis; this means that our line is parallel to the \[y\] - axis.
We need a line that passes through the point \[\left( { - 4,0} \right)\]and is parallel to the \[y\] - axis. We will represent this condition on the graph:

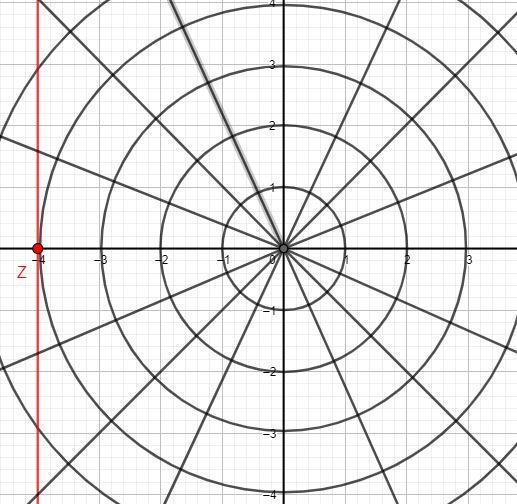
We can see from the graph that the required line is \[x = - 4\].
We will convert the notation of this line to polar coordinates. We will substitute \[ - 4\] for \[x\] in the 1st formula:
\[r\cos \theta = - 4\]
$\therefore $ The polar equation of the line passing through \[\left( {4,\dfrac{{2\pi }}{2}} \right)\] and perpendicular to the line joining the origin to this point is \[r\cos \theta = - 4\].

Note: We can also find the polar equation of the line using the formula \[r\cos \left( {\theta - \alpha } \right) = p\] where \[p\] is the length of the normal to the line from the origin and \[\alpha \] is the angle that the line makes with the polar axis. We will substitute 4 for \[p\] and \[\pi \] for \[\alpha \] in the formula for the polar equation of a line:
\[r\cos \left( {\theta - \pi } \right) = 4\].
We know that \[\cos \left( {\theta - \pi } \right) = - \cos \theta \]:
\[\begin{array}{c} \Rightarrow - r\cos \theta = 4\\ \Rightarrow r\cos \theta = - 4\end{array}\]