Question

The points which trisect the line segment joining the points \[\left( 0,0 \right)\] and \[\left( 9,12 \right)\] are
(A) \[\left( 3,4 \right)\]
(B) \[\left( 8,6 \right)\]
(C) \[\left( 6,8 \right)\]
(D) \[\left( 4,0 \right)\]

Answer 1

Hint: Assume the coordinate of the point C be \[\left( {{x}_{1}},{{y}_{1}} \right)\] and the coordinate of the point D be \[\left( {{x}_{2}},{{y}_{2}} \right)\] . The point C is the midpoint of the line joining the points A and D, and the point D is the midpoint of the line joining the points C and B. We know the formula for the midpoint of the line joining two points having coordinates \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] , \[\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)\] . Use this formula and get the coordinates of the points C and D. Then, compare the coordinates of the points C and D with \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] respectively. Now, solve it further and get the values of \[{{x}_{1}}\] , \[{{y}_{1}}\] , \[{{x}_{2}}\] , and \[{{y}_{2}}\] .

Complete step-by-step answer:
According to the question, we have the coordinates of two points which are \[\left( 0,0 \right)\] and \[\left( 9,12 \right)\] .
The coordinate of the point A = \[\left( 0,0 \right)\] ………………..……(1)
The coordinate of the point B = \[\left( 9,12 \right)\] ……………………(2)
For the line AB to be divided into 3 equal parts we need two more points.
Let the coordinate of the point C be \[\left( {{x}_{1}},{{y}_{1}} \right)\] and the coordinate of the point D be \[\left( {{x}_{2}},{{y}_{2}} \right)\] .
The coordinate of the point C = \[\left( {{x}_{1}},{{y}_{1}} \right)\] ………………………..(3)
The coordinate of the point D = \[\left( {{x}_{2}},{{y}_{2}} \right)\] ………………………(4)

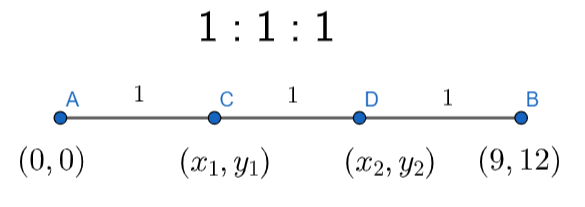
The points C and D are trisecting the line AB. We can say that AC is equal to CD and CD is equal to DB. So,
AC = CD = DB …………………………(5)
We know the formula for the midpoint of the line joining two points having coordinates \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] , \[\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)\] ………………………(6)
For the line AD, we have, AC = CD. It means that the point C \[\left( {{x}_{1}},{{y}_{1}} \right)\] is the midpoint of the line joining the points A \[\left( 0,0 \right)\] and D \[\left( {{x}_{2}},{{y}_{2}} \right)\] .
Now, using equation (6) to obtain the midpoint of the line AD.
\[\left( {{x}_{1}},{{y}_{1}} \right)=\left( \dfrac{0+{{x}_{2}}}{2},\dfrac{0+{{y}_{2}}}{2} \right)\]
\[\Rightarrow \left( {{x}_{1}},{{y}_{1}} \right)=\left( \dfrac{{{x}_{2}}}{2},\dfrac{{{y}_{2}}}{2} \right)\] ……………………..(7)
Comparing the LHS and RHS of equation (7), we get \[{{x}_{1}}=\dfrac{{{x}_{2}}}{2}\] and \[{{y}_{1}}=\dfrac{{{y}_{2}}}{2}\] .
Now, solving
\[{{x}_{1}}=\dfrac{{{x}_{2}}}{2}\]
\[\Rightarrow 2{{x}_{1}}={{x}_{2}}\] ……………….(8)
Now, solving
\[{{y}_{1}}=\dfrac{{{y}_{2}}}{2}\]
\[\Rightarrow 2{{y}_{1}}={{y}_{2}}\] ……………….(9)
For the line CB, we have, CD = DB. It means that the point D \[\left( {{x}_{2}},{{y}_{2}} \right)\] is the midpoint of the line joining the points C \[\left( {{x}_{1}},{{y}_{1}} \right)\] and B \[\left( 9,12 \right)\] .
Now, using equation (6) to obtain the midpoint of the line CB.
\[\left( {{x}_{2}},{{y}_{2}} \right)=\left( \dfrac{{{x}_{1}}+9}{2},\dfrac{{{y}_{1}}+12}{2} \right)\] ……………………..(10)
Comparing the LHS and RHS of equation (10), we get \[{{x}_{2}}=\dfrac{{{x}_{1}}+9}{2}\] and \[{{y}_{2}}=\dfrac{{{y}_{1}}+12}{2}\] .
Now, solving
\[{{x}_{2}}=\dfrac{{{x}_{1}}+9}{2}\]
\[\Rightarrow 2{{x}_{2}}={{x}_{1}}+9\] ……………….(11)
Now, putting the value of \[{{x}_{2}}\] from equation (8) in equation (10), we get
\[\begin{align}
  & \Rightarrow 2\left( 2{{x}_{1}} \right)={{x}_{1}}+9 \\
 & \Rightarrow 4{{x}_{1}}={{x}_{1}}+9 \\
 & \Rightarrow 4{{x}_{1}}-{{x}_{1}}=9 \\
 & \Rightarrow 3{{x}_{1}}=9 \\
\end{align}\]
\[\Rightarrow {{x}_{1}}=3\] …………………….(12)
Putting the value of \[{{x}_{1}}\] in equation (8), we get
\[\begin{align}
  & \Rightarrow 2{{x}_{1}}={{x}_{2}} \\
 & \Rightarrow 2.3={{x}_{2}} \\
\end{align}\]
\[\Rightarrow 6={{x}_{2}}\] ……………………….(13)
 Now, solving
\[{{y}_{2}}=\dfrac{{{y}_{1}}+12}{2}\]
\[\Rightarrow 2{{y}_{2}}={{y}_{1}}+12\] ……………….(14)
Now, putting the value of \[{{y}_{2}}\] from equation (9) in equation (14), we get
\[\begin{align}
  & \Rightarrow 2\left( 2{{y}_{1}} \right)={{y}_{1}}+12 \\
 & \Rightarrow 4{{y}_{1}}={{y}_{1}}+12 \\
 & \Rightarrow 4{{y}_{1}}-{{y}_{1}}=12 \\
 & \Rightarrow 3{{y}_{1}}=12 \\
\end{align}\]
\[\Rightarrow {{y}_{1}}=4\] …………………..(15)
Putting the value of \[{{y}_{1}}\] in equation (8), we get
\[\begin{align}
  & \Rightarrow 2{{y}_{1}}={{y}_{2}} \\
 & \Rightarrow 2.4={{y}_{2}} \\
\end{align}\]
\[\Rightarrow 8={{y}_{2}}\] ………………..(16)
From equation (12), equation (13), equation (15), and equation (16), we have the values of \[{{x}_{1}}\] , \[{{y}_{1}}\] , \[{{x}_{2}}\] , and \[{{y}_{2}}\] .
The coordinate of the point C = \[\left( {{x}_{1}},{{y}_{1}} \right)\] = \[\left( 3,4 \right)\] .
The coordinate of the point D = \[\left( {{x}_{2}},{{y}_{2}} \right)\] = \[\left( 6,8 \right)\] .
Hence, the correct option is (C) and (D).

Note: We can also solve this question by using section formula.
We know the formula that the coordinate of a point which divides the line joining two point
\[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] in the ratio m:n is, \[\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)\] ……………….(1)
Let the coordinate of the point C be \[\left( {{x}_{1}},{{y}_{1}} \right)\] and the coordinate of the point D be \[\left( {{x}_{2}},{{y}_{2}} \right)\] .
The coordinate of the point C = \[\left( {{x}_{1}},{{y}_{1}} \right)\] ………………………..(2)
The coordinate of the point D = \[\left( {{x}_{2}},{{y}_{2}} \right)\] ………………………(3)

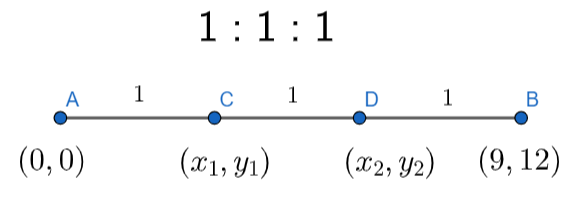
In the figure we can see that AC = CD = DB. So, we can say that the point C \[\left( {{x}_{1}},{{y}_{1}} \right)\] is dividing the line AB ratio 1:2 and the point D \[\left( {{x}_{2}},{{y}_{2}} \right)\]is dividing the line AB in the ratio 2:1.

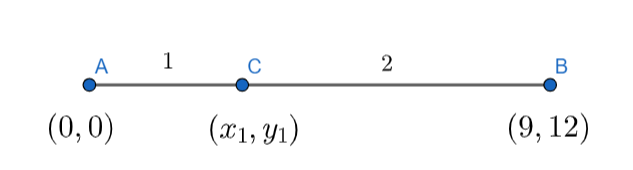
The point C \[\left( {{x}_{1}},{{y}_{1}} \right)\] is dividing the line joining the points A \[\left( 0,0 \right)\] and B \[\left( 9,12 \right)\] in the ratio 1:2.
Using, equation (1), we can get the coordinates of the point C \[\left( {{x}_{1}},{{y}_{1}} \right)\] .
\[\begin{align}
  & \left( {{x}_{1}},{{y}_{1}} \right)=\left( \dfrac{1\times 9+2\times 0}{1+2},\dfrac{1\times 12+2\times 0}{1+2} \right) \\
 & \Rightarrow \left( {{x}_{1}},{{y}_{1}} \right)=\left( \dfrac{9}{3},\dfrac{12}{3} \right) \\
 & \Rightarrow \left( {{x}_{1}},{{y}_{1}} \right)=\left( 3,4 \right) \\
\end{align}\]

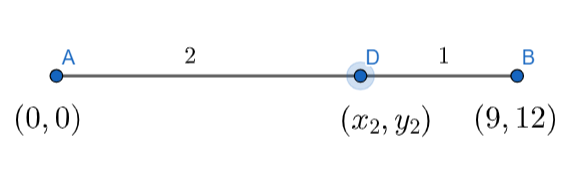
The point D \[\left( {{x}_{2}},{{y}_{2}} \right)\] is dividing the line joining the points A \[\left( 0,0 \right)\] and B \[\left( 9,12 \right)\] in the ratio 2:1.
Using, equation (1), we can get the coordinates of the point D \[\left( {{x}_{2}},{{y}_{2}} \right)\] .
\[\begin{align}
  & \left( {{x}_{2}},{{y}_{2}} \right)=\left( \dfrac{2\times 9+1\times 0}{1+2},\dfrac{2\times 12+1\times 0}{1+2} \right) \\
 & \Rightarrow \left( {{x}_{2}},{{y}_{2}} \right)=\left( \dfrac{18}{3},\dfrac{24}{3} \right) \\
 & \Rightarrow \left( {{x}_{2}},{{y}_{2}} \right)=\left( 6,8 \right) \\
\end{align}\]
The coordinate of the point C = \[\left( {{x}_{1}},{{y}_{1}} \right)\] = \[\left( 3,4 \right)\] .
The coordinate of the point D = \[\left( {{x}_{2}},{{y}_{2}} \right)\] = \[\left( 6,8 \right)\] .
Hence, the correct option is (C) and (D).