
The points \[A\left( {12,8} \right)\], \[B\left( { - 2,6} \right)\] and \[C\left( {6,0} \right)\] are vertices of
A. Right-angled triangle
B. Isosceles triangle
C. Equilateral triangle
D. None of these
Answer
574.5k+ views
Hint: We need to find the distance between the points. This distance is nothing but the length of that side of that triangle. These lengths will help us in identifying the type of triangle. To find the distance between the points using the distance formula.
Formula used:
\[d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \]
Complete step by step answer:
Given vertices of that triangle are \[A\left( {12,8} \right),B\left( { - 2,6} \right) and C\left( {6,0} \right)\].
Now let’s find the distance between them one by one.
That is distance AB, BC and CA.
\[d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \]
\[\begin{gathered}
d(AB) = \sqrt {{{\left( { - 2 - 12} \right)}^2} + {{\left( {6 - 8} \right)}^2}} \\
\Rightarrow \sqrt {{{( - 14)}^2} + {{( - 2)}^2}} \\
\Rightarrow \sqrt {196 + 4} \\
\Rightarrow \sqrt {200} \\
\Rightarrow 10\sqrt 2 \\
\end{gathered} \]
Then,
\[\begin{gathered}
d(BC) = \sqrt {{{\left( {6 - ( - 2)} \right)}^2} + {{\left( {0 - 6} \right)}^2}} \\
\Rightarrow \sqrt {{{(8)}^2} + {{( - 6)}^2}} \\
\Rightarrow \sqrt {64 + 36} \\
\Rightarrow \sqrt {100} \\
\Rightarrow 10 \\
\end{gathered} \]
And at last,
\[\begin{gathered}
d(CA) = \sqrt {{{\left( {6 - 12} \right)}^2} + {{(0 - 8)}^2}} \\
\Rightarrow \sqrt {{{( - 6)}^2} + {{( - 8)}^2}} \\
\Rightarrow \sqrt {36 + 64} \\
\Rightarrow \sqrt {100} \\
\Rightarrow 10 \\
\end{gathered} \]
Since two lengths are same that must be an isosceles triangle.
Thus, option b is correct.
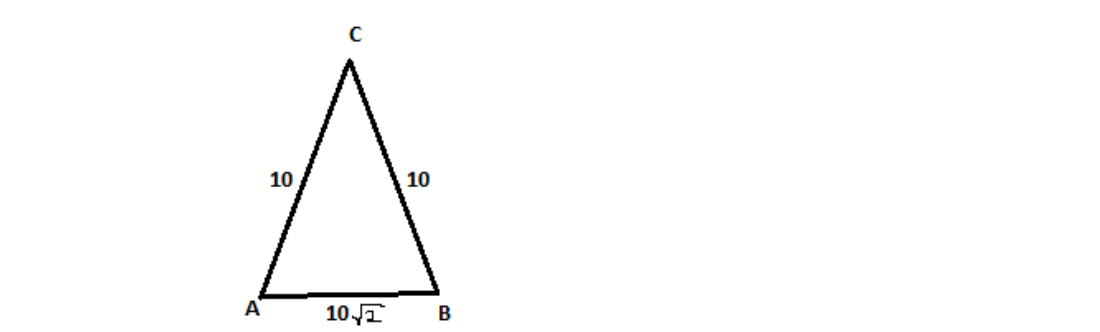
Note: Students should find all the distances or we can say lengths of sides of the triangle. They should not judge the type of triangle just by finding any two sides of the triangle. In problems like these if you get all the three distances equal then it is an equilateral triangle. To find whether it is a right-angled triangle using the Pythagoras theorem.
\[{(hypt)^2} = {(base)^2} + {(height)^2}\]. One side will be your hypotenuse and the remaining two will form base and height.
Additional information:
An equilateral triangle is a triangle having all sides equal. Each angle of the equilateral triangle is of \[{60^ \circ }\].
An isosceles triangle is a triangle having any two sides of the same length. The base angles of the triangle are the same.
The right-angled triangle is having one of the angles \[{90^ \circ }\] and the remaining two are acute angles.
Formula used:
\[d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \]
Complete step by step answer:
Given vertices of that triangle are \[A\left( {12,8} \right),B\left( { - 2,6} \right) and C\left( {6,0} \right)\].
Now let’s find the distance between them one by one.
That is distance AB, BC and CA.
\[d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \]
\[\begin{gathered}
d(AB) = \sqrt {{{\left( { - 2 - 12} \right)}^2} + {{\left( {6 - 8} \right)}^2}} \\
\Rightarrow \sqrt {{{( - 14)}^2} + {{( - 2)}^2}} \\
\Rightarrow \sqrt {196 + 4} \\
\Rightarrow \sqrt {200} \\
\Rightarrow 10\sqrt 2 \\
\end{gathered} \]
Then,
\[\begin{gathered}
d(BC) = \sqrt {{{\left( {6 - ( - 2)} \right)}^2} + {{\left( {0 - 6} \right)}^2}} \\
\Rightarrow \sqrt {{{(8)}^2} + {{( - 6)}^2}} \\
\Rightarrow \sqrt {64 + 36} \\
\Rightarrow \sqrt {100} \\
\Rightarrow 10 \\
\end{gathered} \]
And at last,
\[\begin{gathered}
d(CA) = \sqrt {{{\left( {6 - 12} \right)}^2} + {{(0 - 8)}^2}} \\
\Rightarrow \sqrt {{{( - 6)}^2} + {{( - 8)}^2}} \\
\Rightarrow \sqrt {36 + 64} \\
\Rightarrow \sqrt {100} \\
\Rightarrow 10 \\
\end{gathered} \]
Since two lengths are same that must be an isosceles triangle.
Thus, option b is correct.
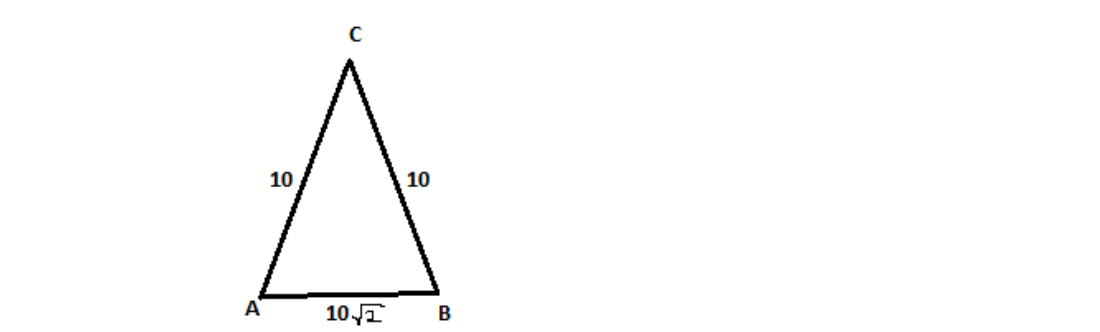
Note: Students should find all the distances or we can say lengths of sides of the triangle. They should not judge the type of triangle just by finding any two sides of the triangle. In problems like these if you get all the three distances equal then it is an equilateral triangle. To find whether it is a right-angled triangle using the Pythagoras theorem.
\[{(hypt)^2} = {(base)^2} + {(height)^2}\]. One side will be your hypotenuse and the remaining two will form base and height.
Additional information:
An equilateral triangle is a triangle having all sides equal. Each angle of the equilateral triangle is of \[{60^ \circ }\].
An isosceles triangle is a triangle having any two sides of the same length. The base angles of the triangle are the same.
The right-angled triangle is having one of the angles \[{90^ \circ }\] and the remaining two are acute angles.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




