
The points (2, 3), (1, 5), (3, -2) are the vertices of a triangle. Find the centroid.
Answer
622.5k+ views
HINT: - The centroid is the centre point of the object. The point in which the three medians of the triangle intersect is known as the centroid of the triangle. It is also defined as the point of intersection of all the three medians. The median is a line that joins the midpoint of a side and the opposite vertex of the triangle. The centroid of the triangle separates the median in the ratio of 2: 1.
Complete step-by-step solution -
It can be found by taking the average of x- coordinate points and y-coordinate points of all the vertices of the triangle.
Hence, the formula for calculating the centroid of a triangle is given as follows
\[\left( {{x}_{G}},{{y}_{G}} \right)=\left[ \left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3} \right),\left( \dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right) \right]\]
(Where the vertices of the triangle are \[\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)\ and\ \left( {{x}_{3}},{{y}_{3}} \right)\] )
As mentioned in the question, we have to find the coordinates of the centroid of a triangle and for this we will use the formula mentioned in the hint which is as follows
\[\left( {{x}_{G}},{{y}_{G}} \right)=\left[ \left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3} \right),\left( \dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right) \right]\]
Now, as the vertices of the triangle are given as
(2, 3), (1, 5) and (3, -2)
Hence, the centroid of this triangle will be
\[\begin{align}
& \left( {{x}_{G}},{{y}_{G}} \right)=\left[ \left( \dfrac{2+1+3}{3} \right),\left( \dfrac{3+5+-2}{3} \right) \right] \\
& \left( {{x}_{G}},{{y}_{G}} \right)=\left[ \left( \dfrac{6}{3} \right),\left( \dfrac{6}{3} \right) \right] \\
& \left( {{x}_{G}},{{y}_{G}} \right)=\left( 2,2 \right) \\
\end{align}\]
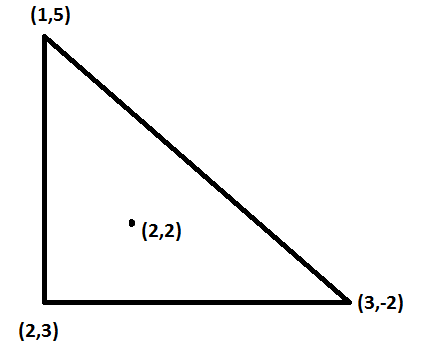
Hence, the centroid of the triangle is at (2, 2).
NOTE: - The students can make a mistake if they don’t know that the centroid is the centre point of the object. The point in which the three medians of the triangle intersect is known as the centroid of triangle and it can be found by taking the average of x- coordinate points and y-coordinate points of all the vertices of the triangle and this formula can be represented as \[\left( {{x}_{G}},{{y}_{G}} \right)=\left[ \left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3} \right),\left( \dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right) \right]\].
Complete step-by-step solution -
It can be found by taking the average of x- coordinate points and y-coordinate points of all the vertices of the triangle.
Hence, the formula for calculating the centroid of a triangle is given as follows
\[\left( {{x}_{G}},{{y}_{G}} \right)=\left[ \left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3} \right),\left( \dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right) \right]\]
(Where the vertices of the triangle are \[\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)\ and\ \left( {{x}_{3}},{{y}_{3}} \right)\] )
As mentioned in the question, we have to find the coordinates of the centroid of a triangle and for this we will use the formula mentioned in the hint which is as follows
\[\left( {{x}_{G}},{{y}_{G}} \right)=\left[ \left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3} \right),\left( \dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right) \right]\]
Now, as the vertices of the triangle are given as
(2, 3), (1, 5) and (3, -2)
Hence, the centroid of this triangle will be
\[\begin{align}
& \left( {{x}_{G}},{{y}_{G}} \right)=\left[ \left( \dfrac{2+1+3}{3} \right),\left( \dfrac{3+5+-2}{3} \right) \right] \\
& \left( {{x}_{G}},{{y}_{G}} \right)=\left[ \left( \dfrac{6}{3} \right),\left( \dfrac{6}{3} \right) \right] \\
& \left( {{x}_{G}},{{y}_{G}} \right)=\left( 2,2 \right) \\
\end{align}\]
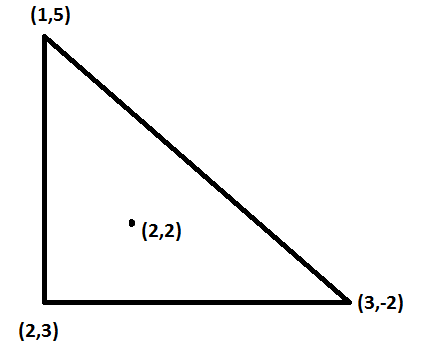
Hence, the centroid of the triangle is at (2, 2).
NOTE: - The students can make a mistake if they don’t know that the centroid is the centre point of the object. The point in which the three medians of the triangle intersect is known as the centroid of triangle and it can be found by taking the average of x- coordinate points and y-coordinate points of all the vertices of the triangle and this formula can be represented as \[\left( {{x}_{G}},{{y}_{G}} \right)=\left[ \left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3} \right),\left( \dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right) \right]\].
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
Who is known as the "Little Master" in Indian cricket history?

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Who Won 36 Oscar Awards? Record Holder Revealed

Why is there a time difference of about 5 hours between class 10 social science CBSE

Explain the Treaty of Vienna of 1815 class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE




