Question

The point of the form \[\left( a,-a \right)\] always lies on the line
(a) $x=a$
(b) $y=a$
(c) $y=x$
(d) $x+y=0$

Answer 1

Hint: We will look at the nature of the lines represented by the equations given in the options. We will use rough diagrams for this purpose. Then we will check which equation is satisfied by the given point. We will substitute the values of the coordinates in the equation of line. The equation that is satisfied by the given point is the line on which the point lies.

Complete step-by-step answer:
The given point is $\left( a,-a \right)$. The first option is the equation $x=a$. This equation tells us that the line it represents is parallel to the y-axis. Let us draw a rough diagram which represents this equation.

On the line $x=a$, every point has the x-coordinate as $a$. So, the points on this line are of the form $\left( a,y \right)$. So, the point $\left( a,-a \right)$ will lie on this line.
Now, the second option is $y=a$. This equation represents a line that is parallel to the x-axis. So, similar to the first equation, every point on this line has the y-coordinate as $a$. Since the points on this line look like $\left( x,a \right)$, the point $\left( a,-a \right)$ does not lie on this line.
The next option is $y=x$. The coordinates of the points lying on this line will have to be equal. Since $a\ne -a$, the point $\left( a,-a \right)$ does not lie on this line.
The last option is$x+y=0$. If we substitute $\left( a,-a \right)$ in this equation, we get $LHS=a+\left( -a \right)=a-a=0=RHS$
Hence, $\left( a,-a \right)$lies on this line. The rough diagram for this equation looks like the following,
 

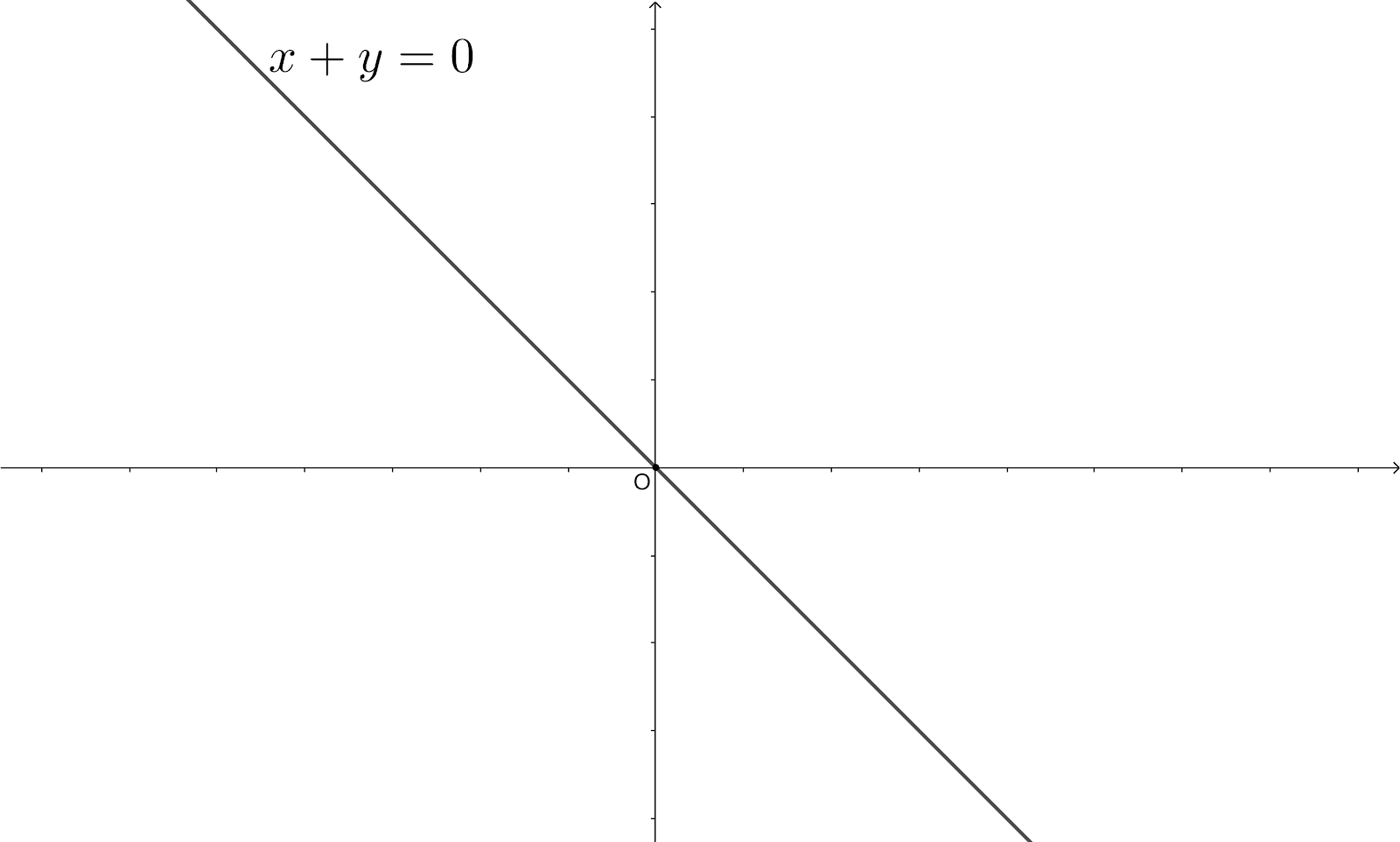
So, the correct options are (a) and (d).

So, the correct answer is “Option (a) and (d)”.

Note: If only one option needs to be selected, then either (a) or (d) is correct. Both the equations are satisfied by the given point which can be checked by substitution or graphing. It is useful to draw rough diagrams for such type of questions. Visual interpretation of equations is always helpful. We should check the equations algebraically as well as by graphing.