Question

The point of concurrency of three altitude of a triangle is called its
A. Incenter
B. Circumcenter
C. Centroid
D. Orthocenter

Answer 1

Hint: First we have to know about the altitude of a triangle. A line from a vertex of a triangle which is perpendicular to the opposite side of a triangle is known as altitude or height of a triangle. So, there are a total of three altitudes in a triangle. Also, the point of concurrency is intersection of or more lines at a point. Using this information, we can try to figure out the correct option.

Complete step by step solution:
We have been asked to find the point of concurrency of three altitudes of a triangle.
We know that the altitude of a triangle is a perpendicular drawn from a vertex to its opposite side. So, it is clear to us that since there are three vertices, there will be a total of three altitudes in a triangle.

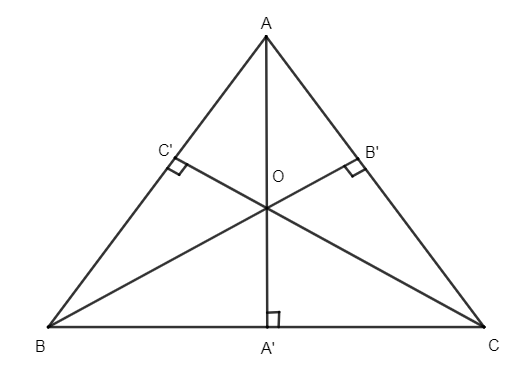
Let us suppose a \[\Delta ABC\] having altitude \[AA',BB'{\rm{ and CC}}'\] intersecting at a common point say O.
We know that the point of concurrency of three altitudes of a triangle is called orthocenter.
Hence, the point O is the orthocenter of \[\Delta ABC\].
Therefore, the correct option is D.

Note: Remember the other terms related to a triangle like incenter, circumcenter and centroid and their definition, so that you can easily solve this kind of question. Now, we call the intersection point as incentre when all the angle bisectors of the triangle meet at that point. If we consider a circle circumscribing a triangle and if all the perpendicular bisectors of sides of the triangle meet at one point, then we call it the circumcentre. When all the medians of the three sides of a triangle meet at one point, we call that point a centroid. Also, remember that the point of concurrency means a point where all the lines, at least three intersect at a common point.