Question

The perpendicular from A on side BC of a $ \Delta ABC $ intersect BC at D such that DB = 3CD. Prove that $ 2A{{B}^{2}}=2A{{C}^{2}}+B{{C}^{2}} $ .

Answer 1

Hint:
 For solving this sum, we will first draw a diagram in which we have $ \Delta ABC $ and a perpendicular AD on BC. We will suppose BC as x and then find values of CD and DB in terms of x using the given condition DB = 3CD. Then we will use Pythagoras theorem in two right angles formed. Using the equation formed from them, we will find our actual answer.

Complete step by step answer:
Here we are given $ \Delta ABC $ in which AD is perpendicular to BC and DB = 3CD. Our figure looks like this,

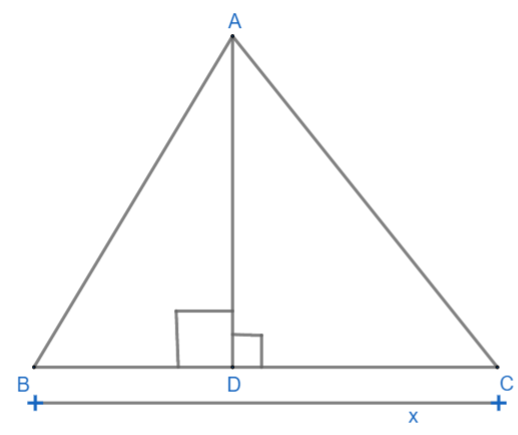
Let us suppose that, BC = x.
As we can see from the diagram BC = CD + DB, therefore x = CD + DB.
We are given that DB = 3CD therefore, $ x=CD+3CD\Rightarrow x=4CD\Rightarrow CD=\dfrac{x}{4} $ .
Using this in DB = 3CD, we get $ DB=3\times \dfrac{x}{4}\Rightarrow DB=\dfrac{3x}{4} $ .
Therefore values of CD is $ \dfrac{x}{4} $ and DB is $ \dfrac{3x}{4} $ .
Now we can see that $ \Delta ABC $ is a right angled triangle. So we can apply Pythagoras theorem according to which $ {{\left( \text{Hypotenuse} \right)}^{2}}={{\left( \text{Base} \right)}^{2}}+{{\left( \text{Perpendicular} \right)}^{2}} $ .
So for $ \Delta ABC $ , $ {{\left( AB \right)}^{2}}={{\left( AD \right)}^{2}}+{{\left( DB \right)}^{2}} $ .
Putting in the values of DB as $ \dfrac{3x}{4} $ we get,
 $ {{\left( AB \right)}^{2}}={{\left( AD \right)}^{2}}+{{\left( \dfrac{3x}{4} \right)}^{2}}\Rightarrow A{{B}^{2}}=A{{D}^{2}}+\dfrac{9{{x}^{2}}}{16}\cdots \cdots \cdots \left( 1 \right) $ .
Also we can see $ \Delta ABC $ is also a right angled triangle. So we can apply Pythagoras theorem here as well, we get, $ {{\left( AC \right)}^{2}}={{\left( AD \right)}^{2}}+{{\left( DC \right)}^{2}} $ .
Putting in the value of BC as $ \dfrac{x}{4} $ we get,
 $ {{\left( AC \right)}^{2}}={{\left( AD \right)}^{2}}+{{\left( \dfrac{x}{4} \right)}^{2}}\Rightarrow A{{C}^{2}}=A{{D}^{2}}+\dfrac{{{x}^{2}}}{16}\cdots \cdots \cdots \left( 2 \right) $ .
Now let us subtract equation (1) from equation (2) we get,
 $ A{{C}^{2}}-A{{B}^{2}}=A{{D}^{2}}+\dfrac{{{x}^{2}}}{16}-\left( A{{D}^{2}}+\dfrac{9{{x}^{2}}}{16} \right) $ .
Simplifying we get,
 $ A{{C}^{2}}-A{{B}^{2}}=A{{D}^{2}}+\dfrac{{{x}^{2}}}{16}-A{{D}^{2}}-\dfrac{9{{x}^{2}}}{16} $ .
Rearranging we have,
 $ A{{C}^{2}}-A{{B}^{2}}=A{{D}^{2}}-A{{D}^{2}}+\dfrac{{{x}^{2}}}{16}-\dfrac{9{{x}^{2}}}{16} $ .
Solving the like terms we get,
 $ A{{C}^{2}}-A{{B}^{2}}=-\dfrac{8{{x}^{2}}}{16} $ .
Simplifying the right-hand side we get,
 $ A{{C}^{2}}-A{{B}^{2}}=\dfrac{-{{x}^{2}}}{2} $ .
Cross multiplying we get,
 $ 2\left( A{{C}^{2}}-A{{B}^{2}} \right)=-{{x}^{2}}\Rightarrow 2A{{C}^{2}}-2A{{B}^{2}}=-{{x}^{2}} $ .
Now we know that x was supposed for BC. So putting x = BC we get,
 $ 2A{{C}^{2}}-2A{{B}^{2}}=-B{{C}^{2}} $ .
Rearranging the terms we get,
 $ 2A{{C}^{2}}+B{{C}^{2}}=2A{{B}^{2}}\Rightarrow 2A{{B}^{2}}=2A{{C}^{2}}+B{{C}^{2}} $ .
Which is our required proof.
Hence proved.

Note:
Students should carefully apply Pythagoras theorem in the right-angled triangle. Take care of signs while solving the equation and subtracting the equation (1) and (2). Make sure to use the proper notation for every side. At last, always arrange the result as given in the question.