Question

The perimeter of a right angled triangle is 72cm and its area is \[216c{{m}^{2}}\]. Find the sum of the lengths of its perpendicular sides (in cm).

Answer 1

Hint: For this problem to solve we have to know the formulas of the area of a triangle, Perimeter of a triangle and by substituting the given values we can get the sum of the lengths of its perpendicular sides. Area of triangle \[=\dfrac{1}{2}ab\], Perimeter of triangle \[=a+b+c\].

Complete step-by-step answer:

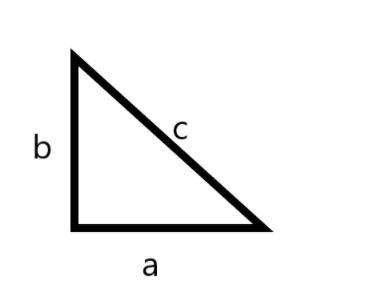
We know the perimeter of a triangle is given by the sum of all sides. Also the value of the perimeter of the triangle is given as 72 cm.
By expressing the above mentioned statement mathematically we get,
\[a+b+c\]= 72 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (1)
We know the area of the triangle is given by the formula \[\dfrac{1}{2}ab=A\], where a is the base and b is the height of the triangle. Also the value of the area of the triangle is given as \[216c{{m}^{2}}\].
By expressing the above mentioned statement mathematically we get,
\[\dfrac{1}{2}ab=216\]
Multiplying with 2 on both sides we get,
ab = 432 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (2)
For a right angled triangle by Pythagoras theorem,
\[{{c}^{2}}={{a}^{2}}+{{b}^{2}}\]. . . . . . . . . . . . . . . . . (a)
\[{{(a+b+c)}^{2}}={{a}^{2}}+{{b}^{2}}+{{c}^{2}}+2ab+2bc+2ca\]
From (a) we are writing,
\[{{(72)}^{2}}={{c}^{2}}+{{c}^{2}}+2ab+2bc+2ca\]
Adding common terms,
\[5184=2{{c}^{2}}+2ab+2bc+2ca\]
Taking 2c as common in the terms,
\[5184=2{{c}^{2}}+2ab+2c(b+a)\]
By substituting the value of (a + b) from (1) we get,
\[5184=2{{c}^{2}}+2ab+2c(72-c)\]
Multiplying with 2c in the last term and expanding,
\[5184=2{{c}^{2}}+2ab+144c-2{{c}^{2}}\]
Simplifying by subtracting the common terms we get,
\[5184=2ab+144c\]
Substituting the value of ab from (2) we get,
\[144c=5184-864\]
\[144c=4320\]
Dividing with 144 on both sides we get,
\[c=\dfrac{4320}{144}\]
\[c=30\]
Now substituting the value of c in (1) we get,
\[a+b+c=72\]
\[a+b+30=72\]
\[a+b=72-30\]
\[a+b=42\]
Hence the sum of the lengths of its perpendicular sides is 42cm.

Note: It is mentioned that everything is in cm we should not convert the units to any form. Here the Pythagoras theorem plays a crucial rule because it was mentioned in question that the given triangle is a right angled triangle. Take care while doing calculations.