Question

The path of train A is given by the equation 3x + 4y — 12 = 0 and the path another train B is given by the equation 6x + 8y — 48 = 0. Represent this situation graphically.

Answer 1

Hint: For system of equations the solution follow some conditions
If there are system of equations, namely $ax+by+c=0$ and $dx+ey+f=0$
Then, $\begin{align}
  & \dfrac{a}{d}=\dfrac{b}{e}=\dfrac{c}{f}\Rightarrow Infinite\text{ }solutions \\
 & \dfrac{a}{d}=\dfrac{b}{e}\ne \dfrac{c}{f}\Rightarrow No\text{ }solutions \\
\end{align}$

Complete step-by-step answer:
Definition of system of equations:
If simultaneously we have more than one equation, then the set of those equations is called a system of equations. We can project systems of equations as lines, planes etc. depending on number of variables.
If we have 2 variables:
Then system of equations is analogous to straight lines
If we have 3 variables:
Then the system of equations is analogous to the planes.
Here we have 2 variables. So, in our case:
Our system of equations is analogous to 2 straight lines.
We have 3 possibilities
(a) No Solutions
(b) Infinite solutions
(c) 1 solution.

(a) No solution:
If two straight lines (infinitely long) have 0 solutions then they must not intersect anywhere that means they are parallel lines.
For 2 lines to be parallel their x – coordinates and y – coordinates must be proportional but constants must not be in proportion to them.
In mathematical way:
If system of equations are
$ax+by+c=0$
$dx+ey+f=0$
then $\begin{align}
  & \dfrac{a}{d}=\dfrac{b}{e}\ne \dfrac{c}{f} \\
 & \Rightarrow No\text{ }Solutions \\
\end{align}$

(b) Infinite solutions
If 2 infinitely long straight lines have infinite solutions then they must be coincident lines, as infinite intersection points implies infinite solutions their x-coordinates, y-coordinates and constants must be in proportion
In mathematical way:
If system of equations are
$\begin{align}
  & ax+by+c=0 \\
 & dx+ey+f=0 \\
\end{align}$
Then $\begin{align}
  & \dfrac{a}{d}=\dfrac{b}{e}=\dfrac{c}{f} \\
 & \Rightarrow Infinite\text{ }Solutions \\
\end{align}$

(c) 1 solution:
If 2 infinitely long straight lines have 1 solution they must be intersecting at only one 1 point.
$\Rightarrow $ If not the above 2 cases then the system of equations satisfy this case.
The paths of two trains are given by equations:
$3x+4y-12=0;$
$6x+8y-48=0$
From above we have, $a=3,b=4,c=-12,d=6,e=8,f=-48$
By substituting in above we get values as
$\dfrac{a}{d}=\dfrac{1}{2},\dfrac{b}{e}=\dfrac{1}{2},\dfrac{c}{f}=\dfrac{1}{4}\Rightarrow \dfrac{a}{b}=\dfrac{b}{e}\ne \dfrac{c}{f}$
No solutions and lines are parallel.
By substituting $y=0$ in 1st line, we get: $3x-12=0\Rightarrow x=4$
By substituting $x=0$ in 1st line, we get: $4y-12=0\Rightarrow y=3$
By substituting $y=0$ in 2nd line we get: $6x-48=0\Rightarrow x=8$
By substituting $x=0$ in 2nd line we get: $8y-48=0\Rightarrow y=6$
To plot graph of 2 parallel line we need 4 points from above we say:
(4, 0); (0, 3) on 1st line
(8, 0); (0,6) on 2nd line

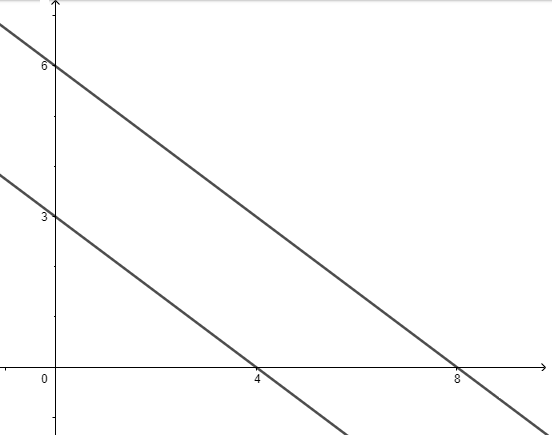
Note: Be careful while assigning points to the line we solved equations by system of equations first, to just check whether our graphical representation is correct or not. We must do it or else we might not know if our graph is correct or not.