
The path of projectile is represented by $y = ax - b{x^2}$ then match the columns:
Column I Column II (i) Range a (ii) Maximum Height a/b (iii) Tangent of angle of projection a^2/4b
(A) (i)-c, (ii)-b, (iii)-a
(B) (i)-b, (ii)-c, (iii)-a
(C) (i)-a, (ii)-c, (iii)-b
(D) (i)-a, (ii)-b, (iii)-c
| Column I | Column II |
| (i) Range | a |
| (ii) Maximum Height | a/b |
| (iii) Tangent of angle of projection | a^2/4b |
Answer
568.2k+ views
Hint: The following equation represents an inward parabola just like a projectile motion of an object thrown at a certain angle with the horizontal. The trajectory equation when differentiated w.r.t x gives the slope of the curve basically telling the point of maximum y (height). The distance between the points where y is zero gives the range. The slope at the starting point x=0, y=0 gives the slope i.e. tangent of angle of projection.
Complete step by step answer:
If an equation of any kind of motion is given whether simple or complex, linear or nonlinear, homogeneous or nonhomogeneous, differential or integral, etc. then a lot of information can be extracted from it. Like here, we will extract three parameters from a single equation. Given,
\[y = ax - b{x^2}\]
The above equation when plotted is as follows:
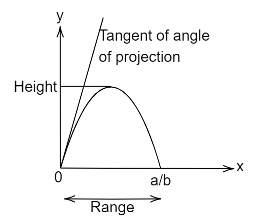
The given equation when differentiated gives the slope:
\[\dfrac{{dy}}{{dx}} = a - 2bx\]
When the slope is zero, that point represents the maximum height as shown in the diagram. The point x when substituted back in equation gives value of y which nothing but the maximum height:
\[
\Rightarrow 0 = a - 2bx \\
\Rightarrow x = \dfrac{a}{{2b}} \\
\Rightarrow y = a\left( {\dfrac{a}{{2b}}} \right) - b\left( {\dfrac{{{a^2}}}{{4{b^2}}}} \right) \\
\Rightarrow y = \dfrac{{{a^2}}}{{4b}} \Rightarrow Height \\
\]
The calculated slope at x=0, y=0 is:
\[
\dfrac{{dy}}{{dx}} = a - 2bx \\
{\left. {\dfrac{{dy}}{{dx}}} \right|_{x = 0}} = a \\
\]
Hence the tangent of angle of projection is at slope m=a.
Mathematically, the distance between the roots of the equation is the range. Substitute y=0 in the equation to get the roots:
\[
\Rightarrow ax - b{x^2} = 0 \\
\Rightarrow x(a - bx) = 0 \\
\Rightarrow x = 0 \\
\therefore x = a/b \\
\]
Therefore, the range is R= a/b-0=a/b.
The correct answer is option B.
Note: In this type of questions, we need not calculate every parameter given in the match the following. From the options we can narrow down the options having different answers for the same option. For example, here we see that if we calculate option (ii) and either (i) or (iii) we would get an answer without solving the whole question. This saves time.
Complete step by step answer:
If an equation of any kind of motion is given whether simple or complex, linear or nonlinear, homogeneous or nonhomogeneous, differential or integral, etc. then a lot of information can be extracted from it. Like here, we will extract three parameters from a single equation. Given,
\[y = ax - b{x^2}\]
The above equation when plotted is as follows:

The given equation when differentiated gives the slope:
\[\dfrac{{dy}}{{dx}} = a - 2bx\]
When the slope is zero, that point represents the maximum height as shown in the diagram. The point x when substituted back in equation gives value of y which nothing but the maximum height:
\[
\Rightarrow 0 = a - 2bx \\
\Rightarrow x = \dfrac{a}{{2b}} \\
\Rightarrow y = a\left( {\dfrac{a}{{2b}}} \right) - b\left( {\dfrac{{{a^2}}}{{4{b^2}}}} \right) \\
\Rightarrow y = \dfrac{{{a^2}}}{{4b}} \Rightarrow Height \\
\]
The calculated slope at x=0, y=0 is:
\[
\dfrac{{dy}}{{dx}} = a - 2bx \\
{\left. {\dfrac{{dy}}{{dx}}} \right|_{x = 0}} = a \\
\]
Hence the tangent of angle of projection is at slope m=a.
Mathematically, the distance between the roots of the equation is the range. Substitute y=0 in the equation to get the roots:
\[
\Rightarrow ax - b{x^2} = 0 \\
\Rightarrow x(a - bx) = 0 \\
\Rightarrow x = 0 \\
\therefore x = a/b \\
\]
Therefore, the range is R= a/b-0=a/b.
The correct answer is option B.
Note: In this type of questions, we need not calculate every parameter given in the match the following. From the options we can narrow down the options having different answers for the same option. For example, here we see that if we calculate option (ii) and either (i) or (iii) we would get an answer without solving the whole question. This saves time.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE




