Question

The parallelogram ABCD shows the points P and Q dividing each of the line AD and DC in the ratio 1:4. What is the ratio in which R divides DB? What is the ratio in which R divides PQ?

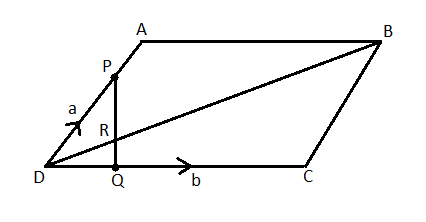
Answer 1

Hint: First construct the line AQ parallel to PQ. Using similar triangles DPQ and DAQ. There are many types of theorems like cevian theorem to get the ratio of the DB and PQ which pass through R.

Complete step by step answer:
Let $\left| {ABC} \right|$ denote area of $\vartriangle ABC$
Let $\left| {ABCD} \right| = 10x$,
$ \Rightarrow \left| {ABC} \right| = \left| {ADC} \right| = \left| {ABD} \right| = \left| {CBD} \right| = \dfrac{{10x}}{2} = 5x$
Given, $DQ:QC = 1:4$,
$ \Rightarrow \left| {ADQ} \right|:\left| {AQC} \right| = \left| {BDQ} \right|\left| {BQC} \right| = 1:4$,
$ \Rightarrow \left| {ABP} \right| = x,\left| {PBD} \right| = 4x$,
And, $\left| {AQP} \right| = \dfrac{1}{5}x,\left| {PQD} \right| = \dfrac{4}{5}x$
$\left| {PDQB} \right| = \left| {PBD} \right| + \left| {BDQ} \right| = 4x + x = 5x$
$ \Rightarrow \left| {PQB} \right| = \left| {PDQB} \right| - \left| {PDQ} \right| = 5x - \dfrac{4}{5}x = \dfrac{{21}}{5}x$
$ \Rightarrow DR:RB = \left| {PDQ} \right|:\left| {PQB} \right| = \dfrac{4}{5}x:\dfrac{{21}}{5}x = 4:21$
$\therefore PR:RQ = \left| {BPD} \right|:\left| {BDQ} \right| = 4x:x = 4:1$

Note: One may note that there are certain quadrilaterals whose diagonals bisect each other but here we have assumed the quadrilateral as a parallelogram because this is the basic property of a parallelogram.