
The orthocenter of the triangle $ABC$ is $B$ and the circumcenter is $S(a,b)$. If $A$ is the origin then the coordinates of $C$ are
A: $(2a,2b)$
B: $\left( {\dfrac{a}{2},\dfrac{b}{2}} \right)$
C: $\left( {\sqrt {{a^2} + {b^2}} ,0} \right)$
D: None
Answer
555.6k+ views
Hint:
Whenever they give orthocenter of a triangle then the triangle will be a right angled triangle and in the above question the circumcenter which is nothing but midpoint is given, so by using mid-point theorem formula that is Mid-point$ = \left[ {\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)} \right]$we can find the coordinates of $C$.
Complete step by step solution:
Before going to solve the problem, let us understand the problem statement:
In this question they have given the orthocenter of a triangle $ABC$ is $B$, from this it is clear that whenever an orthocenter is given then the triangle is a right angled triangle. Therefore the triangle $ABC$ is a right angled triangle at a point B(as shown is below figure).
It is given that $A$ is the origin which means the coordinates of $A$that is $({x_1},{y_1})$will be $(0,0)$.
Let us consider C coordinates that are $({x_2},{y_2})$ be $(x,y)$.
Now, they have given the circumcenter (these are the lines that are right angles to the midpoint of each side) as $S(a,b)$. For a right angled triangle the circumcenter is the midpoint of the hypotenuse. So now $S(a,b)$lies in the middle of the hypotenuse that is $AC$ as shown in the diagram below.
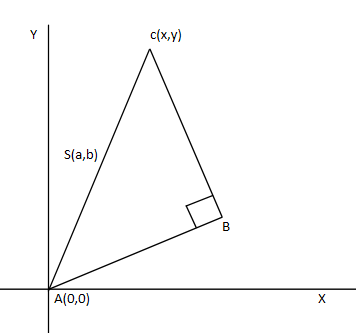
Now by using the midpoint theorem formula we can find the coordinates of $C$.
The midpoint formula is given by:
Mid-point$ = \left[ {\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)} \right]$ …….equation 1
Where $({x_1},{y_1})$ is coordinates of point$A$which is $(0,0)$
$({x_2},{y_2})$ is coordinates of point C which is $(x,y)$
Now, substituting the values of ${x_1},{x_2},{y_1},{y_2}$ and midpoint that is$S(a,b)$in the above equation 1,
we get
$S(a,b) = \left[ {\dfrac{{0 + x}}{2},\dfrac{{0 + y}}{2}} \right]$
By comparing both the sides, we get
$a = \dfrac{x}{2}$ and $b = \dfrac{y}{2}$
Therefore we can say that,
$x = 2a$ and $y = 2b$.
Hence the required coordinates of point $C$ is $(2a,2b)$.
Note:
Whenever we take the coordinates of a point we should observe carefully that it is not always the case that they give origin as coordinates for a point, there may be other cases as well.
Sometimes they may give the coordinates of $C$ and can ask to solve for circumcenter or mid-point.
Whenever they give orthocenter of a triangle then the triangle will be a right angled triangle and in the above question the circumcenter which is nothing but midpoint is given, so by using mid-point theorem formula that is Mid-point$ = \left[ {\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)} \right]$we can find the coordinates of $C$.
Complete step by step solution:
Before going to solve the problem, let us understand the problem statement:
In this question they have given the orthocenter of a triangle $ABC$ is $B$, from this it is clear that whenever an orthocenter is given then the triangle is a right angled triangle. Therefore the triangle $ABC$ is a right angled triangle at a point B(as shown is below figure).
It is given that $A$ is the origin which means the coordinates of $A$that is $({x_1},{y_1})$will be $(0,0)$.
Let us consider C coordinates that are $({x_2},{y_2})$ be $(x,y)$.
Now, they have given the circumcenter (these are the lines that are right angles to the midpoint of each side) as $S(a,b)$. For a right angled triangle the circumcenter is the midpoint of the hypotenuse. So now $S(a,b)$lies in the middle of the hypotenuse that is $AC$ as shown in the diagram below.
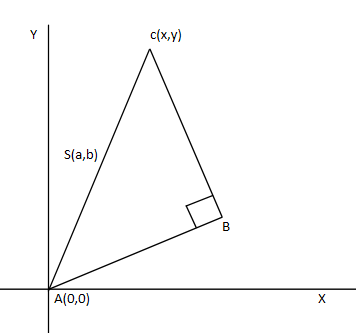
Now by using the midpoint theorem formula we can find the coordinates of $C$.
The midpoint formula is given by:
Mid-point$ = \left[ {\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)} \right]$ …….equation 1
Where $({x_1},{y_1})$ is coordinates of point$A$which is $(0,0)$
$({x_2},{y_2})$ is coordinates of point C which is $(x,y)$
Now, substituting the values of ${x_1},{x_2},{y_1},{y_2}$ and midpoint that is$S(a,b)$in the above equation 1,
we get
$S(a,b) = \left[ {\dfrac{{0 + x}}{2},\dfrac{{0 + y}}{2}} \right]$
By comparing both the sides, we get
$a = \dfrac{x}{2}$ and $b = \dfrac{y}{2}$
Therefore we can say that,
$x = 2a$ and $y = 2b$.
Hence the required coordinates of point $C$ is $(2a,2b)$.
Note:
Whenever we take the coordinates of a point we should observe carefully that it is not always the case that they give origin as coordinates for a point, there may be other cases as well.
Sometimes they may give the coordinates of $C$ and can ask to solve for circumcenter or mid-point.
Recently Updated Pages
Master Class 8 Maths: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 7 Maths: Engaging Questions & Answers for Success

Class 7 Question and Answer - Your Ultimate Solutions Guide

Master Class 6 Maths: Engaging Questions & Answers for Success

Class 6 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Which of the following does not have a fundamental class 10 physics CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




