Question

The orthocenter of a right-angled triangle is formed
(A). Inside the triangle
(B). On the hypotenuse of the triangle
(C). Behind the right angle of the triangle
(D). On the right vertex of the triangle

Answer 1

Hint: First look at the definition of orthocenter and required terms to find the orthocenter. By options check the correct answer. Check the position of the orthocenter exactly to get the right answer related to all terms of definition to the right angled triangle.

Complete step-by-step solution -
Given condition in the question is written as follows below:
Orthocenter of a right angled triangle.
The orthocenter is a point of intersection of all the three altitudes of the triangle.
We know that there are three altitudes of a triangle.

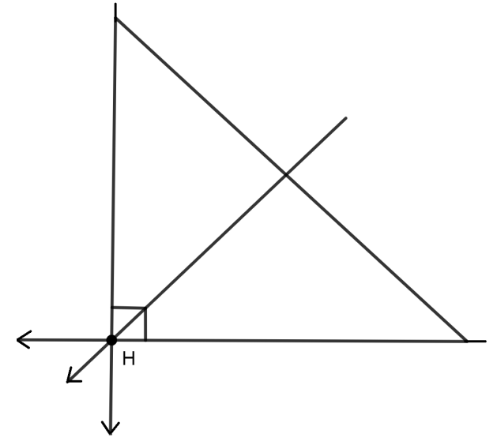
In a right angled triangle two sides are perpendicular.
The line drawn from a vertex which is perpendicular to the opposite side is altitude. The 2 side’s perpendicular will themselves become the altitude of respective vertex.
Now we have 2 altitudes meet at a vertex. The altitude from that vertex will obviously pass through that vertex.
So, by this way we can say the intersection of all the altitudes is the right angle vertex.
So, option (d) is the correct answer.

Note: Generally students confuse between the terms orthocenter, circumcenter. Use the definition properly. While finding altitude the idea of saying both sides all altitudes is very crucial which leads us to the result obtained.