The orbit of the earth is an ellipse with eccentricity $\dfrac{1}{{60}}$ with Sun at one focus, the major axis being approximately $186 \times 1{0^6}\;miles$ in length. The shortest and longest distance of the earth from the Sun is
A.$9145 \times {10^4}\;{\text{miles}}$, $9455 \times {10^4}\;{\text{miles}}$
B.$9147 \times {10^4}\;{\text{miles}}$, $9457 \times {10^4}\;{\text{miles}}$
C.$9145 \times {10^6}\;{\text{miles}}$, $9455 \times {10^6}\;{\text{miles}}$
D.None of these
Verified119.7k+ views
Hint: We know that an ellipse has two foci and the sun is at one focus of the ellipse. First find the length of the semi-major axis of the ellipse. We can find the shortest distance of the earth from the Sun by $d = a\left( {1 - e} \right)$ and the longest distance by $d = a\left( {1 + e} \right)$. Here, $a$ represents the length of the major axis and $e$ is the eccentricity of the ellipse.
Complete step-by-step answer:
We will draw the diagram according to the given information of an ellipse.
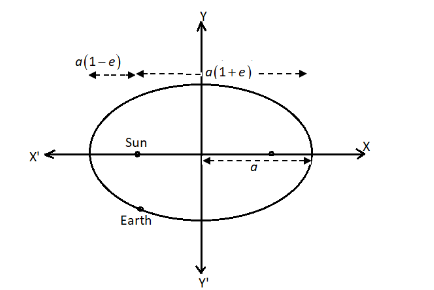
We know that the major part of the orbit that is in the shape of an ellipse is $186 \times 1{0^6}\;miles$. So,
$2a = 186 \times 1{0^6}\;miles$
$\Rightarrow$ $a = \dfrac{{186 \times 1{0^6}\;miles}}{2}$
$\Rightarrow$ $a = 93 \times 1{0^6}\;miles$
It is the semi-major axis of the ellipse. The eccentricity of the ellipse is $e = \dfrac{1}{{60}}$.
The shortest distance of the earth from the Sun is given by,
$d = a\left( {1 - e} \right)$
Put the values of $a$ and $e$ in the above formula, we get
$\Rightarrow$ $d = 93 \times {10^6}{\text{miles}}\left( {1 - \dfrac{1}{{60}}} \right)$
$\Rightarrow$ $d = 93 \times {10^6}{\text{miles}}\left( {\dfrac{{59}}{{60}}} \right)$
$\Rightarrow$ $d = \dfrac{{5487 \times {{10}^5}{\text{miles}}}}{5}$
$\Rightarrow$ $d = 914.5 \times {10^5}{\text{miles}}$
$\Rightarrow$ $d = 9145 \times {10^4}{\text{miles}}$
Now, the longest distance of the earth from the Sun is given by,
$d = a\left( {1 + e} \right)$
Put the values of $a$ and $e$ in the above formula, we get
$\Rightarrow$ $d = 93 \times {10^6}{\text{miles}}\left( {1 + \dfrac{1}{{60}}} \right)$
$\Rightarrow$ $d = 93 \times {10^6}{\text{miles}}\left( {\dfrac{{61}}{{60}}} \right)$
$\Rightarrow$ $d = \dfrac{{5673 \times {{10}^5}{\text{miles}}}}{5}$
$\Rightarrow$ $d = 945.5 \times {10^5}{\text{miles}}$
$\Rightarrow$ $d = 9455 \times {10^4}{\text{miles}}$
Therefore, the shortest length of the earth from the Sun is $9145 \times {10^4}{\text{miles}}$ and the longest length of the earth from the Sun is $9455 \times {10^4}\;{\text{miles}}$.
So, the option (A) is the correct answer.
Note: By Kepler's law of planetary motion, it can be stated that the shape of the path of the planet's orbit is an ellipse with the Sun at one of its foci. The point which is closest to the Sun in this orbit is known as perihelion and the point which is farthest to the Sun in this orbit is known as aphelion.
Complete step-by-step answer:
We will draw the diagram according to the given information of an ellipse.
We know that the major part of the orbit that is in the shape of an ellipse is $186 \times 1{0^6}\;miles$. So,
$2a = 186 \times 1{0^6}\;miles$
$\Rightarrow$ $a = \dfrac{{186 \times 1{0^6}\;miles}}{2}$
$\Rightarrow$ $a = 93 \times 1{0^6}\;miles$
It is the semi-major axis of the ellipse. The eccentricity of the ellipse is $e = \dfrac{1}{{60}}$.
The shortest distance of the earth from the Sun is given by,
$d = a\left( {1 - e} \right)$
Put the values of $a$ and $e$ in the above formula, we get
$\Rightarrow$ $d = 93 \times {10^6}{\text{miles}}\left( {1 - \dfrac{1}{{60}}} \right)$
$\Rightarrow$ $d = 93 \times {10^6}{\text{miles}}\left( {\dfrac{{59}}{{60}}} \right)$
$\Rightarrow$ $d = \dfrac{{5487 \times {{10}^5}{\text{miles}}}}{5}$
$\Rightarrow$ $d = 914.5 \times {10^5}{\text{miles}}$
$\Rightarrow$ $d = 9145 \times {10^4}{\text{miles}}$
Now, the longest distance of the earth from the Sun is given by,
$d = a\left( {1 + e} \right)$
Put the values of $a$ and $e$ in the above formula, we get
$\Rightarrow$ $d = 93 \times {10^6}{\text{miles}}\left( {1 + \dfrac{1}{{60}}} \right)$
$\Rightarrow$ $d = 93 \times {10^6}{\text{miles}}\left( {\dfrac{{61}}{{60}}} \right)$
$\Rightarrow$ $d = \dfrac{{5673 \times {{10}^5}{\text{miles}}}}{5}$
$\Rightarrow$ $d = 945.5 \times {10^5}{\text{miles}}$
$\Rightarrow$ $d = 9455 \times {10^4}{\text{miles}}$
Therefore, the shortest length of the earth from the Sun is $9145 \times {10^4}{\text{miles}}$ and the longest length of the earth from the Sun is $9455 \times {10^4}\;{\text{miles}}$.
So, the option (A) is the correct answer.
Note: By Kepler's law of planetary motion, it can be stated that the shape of the path of the planet's orbit is an ellipse with the Sun at one of its foci. The point which is closest to the Sun in this orbit is known as perihelion and the point which is farthest to the Sun in this orbit is known as aphelion.