Question

The number of solutions of the equation $1+\sin x.{{\sin }^{2}}\dfrac{x}{2}=0\left[ -\pi ,\pi \right]$ is,
A. Zero
B. 1
C. 2
D. 3

Answer 1

Hint: In this question we will have to know about the range of \[\sin x\ and\ {{\sin }^{2}}\dfrac{x}{2}\] and by using it we will find the number of solution. We know that, \[-1\le \sin x\le 1\,and\ 0\le {{\sin }^{2}}\dfrac{x}{2}\le 1\] for all values of \[x\].

Complete step-by-step answer:
We have been asked to find the number of solutions of the equation $1+\sin x.{{\sin }^{2}}\dfrac{x}{2}=0\left[ -\pi ,\pi \right]$.
We can see the graph of \[\sin x\ and\ {{\sin }^{2}}\dfrac{x}{2}\] as below,

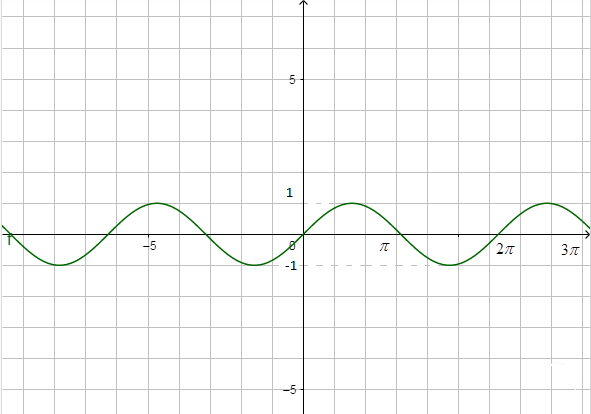
\[\sin x\]

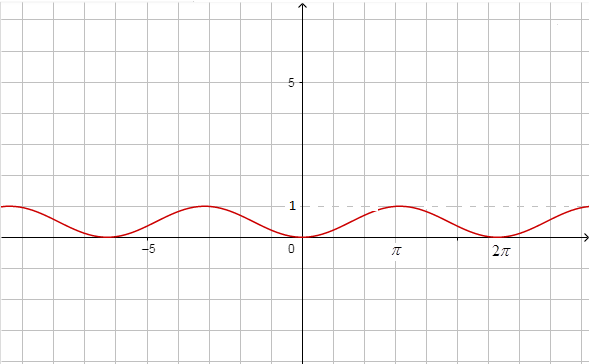
\[{{\sin }^{2}}\dfrac{x}{2}\]
Now, we can observe that for all values of \[x\],
\[\begin{align}
  & -1\le \sin x\le 1\, \\
 & 0\le {{\sin }^{2}}\dfrac{x}{2}\le 1 \\
\end{align}\]
And, \[{{\sin }^{2}}\dfrac{x}{2}\ne \sin x\] for any value of \[x\].
When \[\sin x\] has maximum or minimum value, \[{{\sin }^{2}}\dfrac{x}{2}\] will have less than 1.
So, we can say that $-1<\sin x.{{\sin }^{2}}\dfrac{x}{2}<1$ i.e. the value of the expression $\left( \sin x{{\sin }^{2}}\dfrac{x}{2} \right)$ must be lies between – 1 to 1.
Now, $-1<\sin x.{{\sin }^{2}}\dfrac{x}{2}<1$.
By adding 1 to inequality, we get,
$\begin{align}
  & -1+1<1+\sin x.{{\sin }^{2}}\dfrac{x}{2}<1+1 \\
 & \Rightarrow 0<1+\sin x.{{\sin }^{2}}\dfrac{x}{2}<2 \\
\end{align}$
So, we get the function $f\left( x \right)=1+\sin x.{{\sin }^{2}}\dfrac{x}{2}>0$ for all values of \[x\].
Hence, there will be no any solution of the $f\left( x \right)=0$ i.e., $1+\sin x.{{\sin }^{2}}\dfrac{x}{2}=0$.
Therefore, the correct option is A.

Note: In this type of question try to draw the graph of the function if it is possible as it becomes easy to solve the equation. Also, the graphical method to solve the equation is a shortcut method which you can apply anywhere in these types of questions.