Question

The number of real solutions of the equation $\cos x = {x^2} + x + 1$ is
A. 2
B. 1
C. 0
D. None of these

Answer 1

Hint – In this question, we will proceed by solving the RHS part of the given equation by a complete square method. Then plot a graph between them to know whether they are interesting or not. Then we can find the number of real solutions to the given equation.

Complete step-by-step solution -
Given equation is \[\cos x = {x^2} + x + 1........................\left( 1 \right)\]
Now we will solve equation (1) by completing square method where we will divide and multiply the coefficient of \[x\] with ‘2’
\[ \Rightarrow \cos x = {x^2} + 2 \times \dfrac{x}{2} + 1\]
We can write ‘1’ as \[\dfrac{1}{4} + \dfrac{3}{4}\]. So, we have
\[
   \Rightarrow \cos x = {x^2} + 2 \times \dfrac{x}{2} + \dfrac{1}{4} + \dfrac{3}{4} \\
   \Rightarrow \cos x = {x^2} + 2\left( x \right)\left( {\dfrac{1}{2}} \right) + \dfrac{1}{{{2^2}}} + \dfrac{3}{4} \\
\]
Using the algebraic identity \[{a^2} + 2ab + {b^2} = {\left( {a + b} \right)^2}\], we have
\[\therefore \cos x = {\left( {x + \dfrac{1}{2}} \right)^2} + \dfrac{3}{4}\]
When we plot a graph between \[y = {\left( {x + \dfrac{1}{2}} \right)^2} + \dfrac{3}{4}\] and \[y = \cos x\] we have the graph as

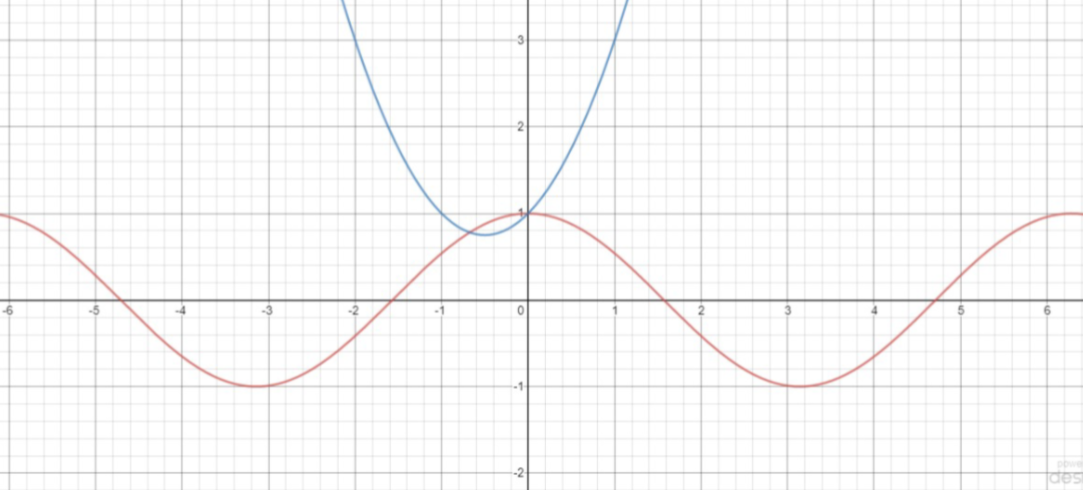
So clearly, they are intersecting at two points.
Hence there are two real solutions to given equation \[\cos x = {x^2} + x + 1\].
Thus, the correct option is A. 2

Note – These kinds of questions must be solved with full concentration and practiced as many times as you can make the mistake in the method used, i.e., Completing the Square Method, which is very confusing as we keep multiplying and dividing different terms with the equation.