Question

The number of common tangent to the circle one of which passes through the origin and cuts off intercepts 2 from each of the axes, and the other circle has the line segment joining the origin and the point (1,1) as a diameter, is
A. 0
B. 1
C. 2
D. 3

Answer 1

Hint: This problem deals with circles, and their tangents. The general form of a circle is given by:${x^2} + {y^2} + 2gx + 2fy + c = 0$, where the center of this circle is $\left( { - g, - f} \right)$, and the radius of this circle is given by $r = \sqrt {{g^2} + {f^2} - c} $. If the circle is passing through two given points then this formula is used, which gives the equation of the circle, which is given below:
$ \Rightarrow \left( {x - {x_1}} \right)\left( {x - {x_2}} \right) + \left( {y - {y_1}} \right)\left( {y - {y_2}} \right) = 0$

Complete step-by-step answer:
Given there are 2 circles, the first circle passes through the origin and cuts off the intercepts 2 from each axis, and the other circle’s diameter passes through the origin and the point (1,1).
We have found the number of common tangents to these circles.
Here both the circles pass through the origin. A figure is shown below.

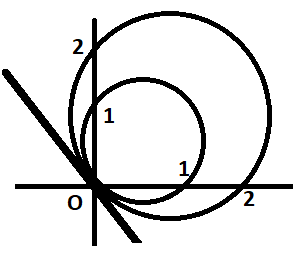
So the general equation of a circle is given by :
$ \Rightarrow {x^2} + {y^2} + 2gx + 2fy + c = 0$
Consider the first circle as it passes through $\left( {0,0} \right),\left( {2,0} \right),\left( {0,2} \right)$. Hence substituting the point $\left( {0,0} \right)$ in the general equation of the circle, to get the value of $c$:
$ \Rightarrow {\left( 0 \right)^2} + {\left( 0 \right)^2} + 2g\left( 0 \right) + 2f\left( 0 \right) + c = 0$
$\therefore c = 0$
Hence the equation of the circle becomes, ${x^2} + {y^2} + 2gx + 2fy = 0$
Now substitute the point $\left( {2,0} \right)$, in the above equation:
$ \Rightarrow {\left( 2 \right)^2} + {\left( 0 \right)^2} + 2g\left( 2 \right) + 2f\left( 0 \right) = 0$
$ \Rightarrow 4 + 4g = 0$
$\therefore g = - 1$
Now substitute the $\left( {0,2} \right)$, in the equation ${x^2} + {y^2} + 2gx + 2fy = 0$, as given below:
\[ \Rightarrow {\left( 0 \right)^2} + {\left( 2 \right)^2} + 2g\left( 0 \right) + 2f\left( 2 \right) = 0\]
$ \Rightarrow 4 + 4f = 0$
$\therefore f = - 1$
Hence the equation of the first circle is given by:
$ \Rightarrow {x^2} + {y^2} - 2x - 2y = 0$
Here $2g = - 2$ and $2f = - 2$
The center of this circle is given by ${c_1} = \left( { - g, - f} \right)$, as given below:
$ \Rightarrow {c_1} = \left( {1,1} \right)$
The radius is given by ${r_1} = \sqrt {{g^2} + {f^2} - c} $, as given below:
$ \Rightarrow {r_1} = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 1} \right)}^2} - 0} $
$ \Rightarrow {r_1} = \sqrt 2 $
Now consider the 2nd circle, as this point passes through the origin$\left( {0,0} \right)$ and the point $\left( {1,1} \right)$, hence the equation of the circle passing through these points is given by:
$ \Rightarrow \left( {x - {x_1}} \right)\left( {x - {x_2}} \right) + \left( {y - {y_1}} \right)\left( {y - {y_2}} \right) = 0$
Here $\left( {{x_1},{y_1}} \right) = \left( {0,0} \right)$ and $\left( {{x_2},{y_2}} \right) = \left( {1,1} \right)$, substituting them in the general equation of circle to get the equation of this circle:
$ \Rightarrow \left( {x - 0} \right)\left( {x - 1} \right) + \left( {y - 0} \right)\left( {y - 1} \right) = 0$
$ \Rightarrow x\left( {x - 1} \right) + y\left( {y - 1} \right) = 0$
Simplifying the above equation, as given below:
$ \Rightarrow {x^2} - x + {y^2} - y = 0$
$ \Rightarrow {x^2} + {y^2} - x - y = 0$
Here $2g = - 1$ and $2f = - 1$
The center of this circle is given by ${c_2} = \left( { - g, - f} \right)$, as given below:
$ \Rightarrow {c_2} = \left( {\dfrac{1}{2},\dfrac{1}{2}} \right)$
The radius is given by ${r_2} = \sqrt {{g^2} + {f^2} - c} $, as given below:
$ \Rightarrow {r_2} = \sqrt {{{\left( { - \dfrac{1}{2}} \right)}^2} + {{\left( { - \dfrac{1}{2}} \right)}^2} - 0} $
$ \Rightarrow {r_2} = \dfrac{1}{{\sqrt 2 }}$
Now we know the centers of the two circles are : ${c_1} = \left( {1,1} \right)$ and ${c_2} = \left( {\dfrac{1}{2},\dfrac{1}{2}} \right)$, the distance between their centers is given by:
$ \Rightarrow {c_1}{c_2} = \sqrt {{{\left( {1 - \dfrac{1}{2}} \right)}^2} + {{\left( {1 - \dfrac{1}{2}} \right)}^2}} $
$ \Rightarrow {c_1}{c_2} = \sqrt {{{\left( { - \dfrac{1}{2}} \right)}^2} + {{\left( { - \dfrac{1}{2}} \right)}^2}} $
On expanding and further simplification of the above expression:
$ \Rightarrow {c_1}{c_2} = \sqrt {\dfrac{1}{4} + \dfrac{1}{4}} = \sqrt {\dfrac{1}{2}} $
$\therefore {c_1}{c_2} = \dfrac{1}{{\sqrt 2 }}$
So the distance between the centers is $\dfrac{1}{{\sqrt 2 }}$.
Now we know the radius of the two circles are: ${r_1} = \sqrt 2 $ and ${r_2} = \dfrac{1}{{\sqrt 2 }}$, the distance between the two radii, is given below:
$ \Rightarrow {r_1} - {r_2} = \sqrt 2 - \dfrac{1}{{\sqrt 2 }}$
$ \Rightarrow {r_1} - {r_2} = \dfrac{{2 - 1}}{{\sqrt 2 }}$
$\therefore {r_1} - {r_2} = \dfrac{1}{{\sqrt 2 }}$
The distance between their centers is equal to the difference of their radii, which is $\dfrac{1}{{\sqrt 2 }}$, which means that these two circles are touching each other internally.
So the no. of common tangents will be equal to 1.

Final Answer: There is only one common tangent for the given two circles.

Note:
 Please note that the equation of a circle can also be represented by the general form, as given by:
$ \Rightarrow {\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2}$
Here the center of the circle is $\left( {a,b} \right)$, and whereas $r$ is the radius of the circle.
This equation of the circle is the same as the general form of the equation which is given by:
$ \Rightarrow {x^2} + {y^2} + 2gx + 2fy + c = 0$