Question

The moon is about 38400 km from the earth and is nearly circular. Find the circumference of the path described by the moon in one complete revolution about the earth. (use \[\pi =3.14\])

Answer 1

Hint: In this question, we first need to draw the diagram because it gives us the clear picture of what we have to find. Then by using the formula of circumference of a circle we can find the circumference of the path described by the moon.
Circumference of a circle is \[2\pi r\]

Complete step-by-step answer:
Let us look at some of the basic definitions first.
CIRCLE: A circle is a set of points which lie in a plane and at a constant distance from a fixed point in the plane.
Radius: Radius is the shortest distance between the centre of the circle and a point on the circumference of the circle.
Chord: A chord is a line joining two points on the circumference of a circle.
Diameter: Diameter is the longest chord of a circle that passes through the centre of the circle. Diameter is twice the radius.
Circumference: The circumference of a circle is defined as the linear distance around it. In other words, if a circle is opened to form a straight line then the length of that line will be the circumference of the circle.
Circumference \[=2\pi r\]
Where, r is the radius of the circle.
Now, let us draw the diagram with the given conditions.

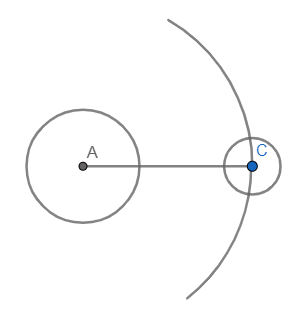
The path described by the moon in one complete revolution is circular which can be observed from the diagram.
 As this path will be nearly circular which gives us that the distance between the earth and the moon acts as the radius for that respective circular path.
Let us assume the circumference of the path as C and radius as r.
\[r=38400\]
\[\begin{align}
  & \Rightarrow C=2\pi r \\
 & \Rightarrow C=2\pi \times 38400 \\
\end{align}\]
\[\begin{align}
  & \Rightarrow C=2\times 3.14\times 38400\text{ }\left[ \because \pi =3.14 \right] \\
 & \therefore C=2,41,152km \\
\end{align}\]
Hence, the circumference of the path described by the moon in one complete revolution is 2,41,152 km.

Note: While calculating the circumference we can either substitute the radius in the formula directly or we can find the diameter of the circular path described for the revolution of the moon and then substitute the value of that obtained diameter in the corresponding formula. Both the methods give the same result.
\[C=\pi d\]
Where, d is the diameter of the circular path.
It is important to note that the circumference of the path formed gives the length of the circular path made by the moon around the earth in one revolution.