Question

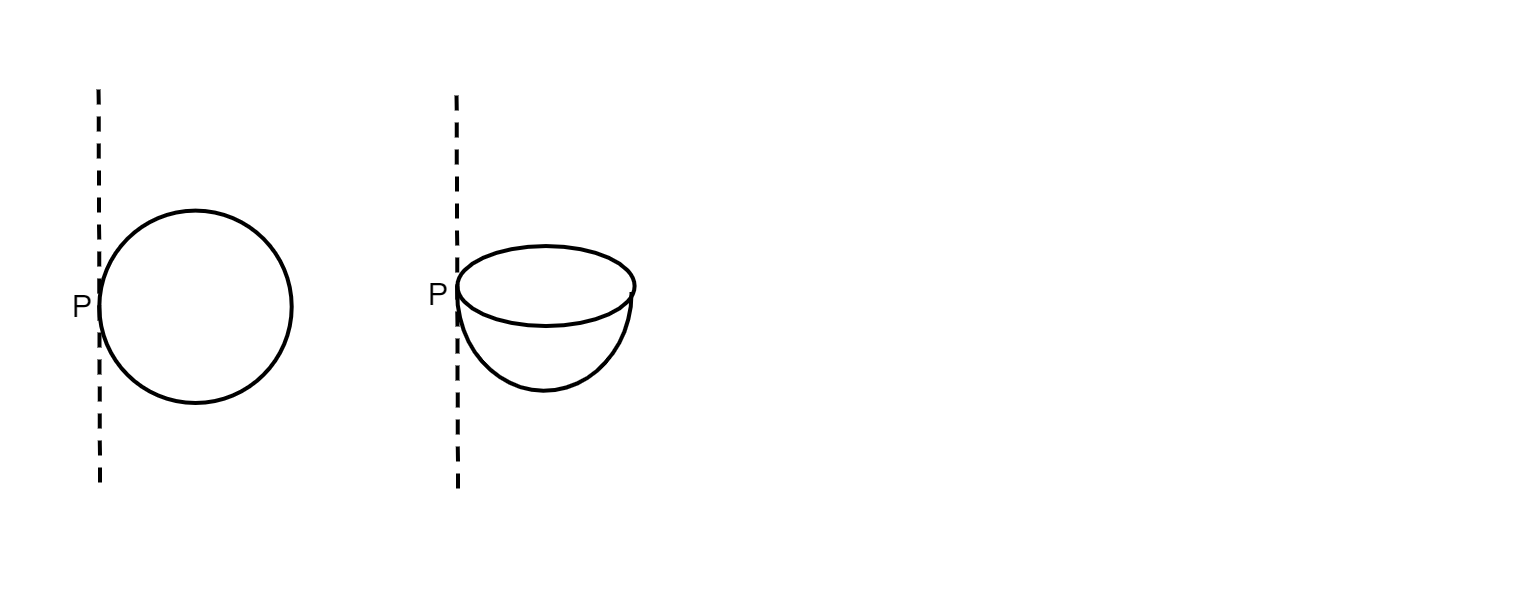
The moment of inertia of a spherical shell and a hemispherical shell of same mass and radius about a tangential axis, passing through $P$ will be

A.Different
B.Same
C.Data insufficient
D.None of these

Answer 1

Hint: To solve this question, we should calculate moment of inertia of both the spherical shell and hemispherical shell separately about a tangential axis and then find out whether the moment of inertia is the same or different. Also, we would have to use parallel axis theorem to find the moment of inertia about a tangential axis.

Complete answer:
The moment of inertia of a spherical shell about an axis passing through its centroid is:
$\dfrac{2}{3}M{{R}^{2}}$
Here, $M$ is the mass of the spherical shell and $R$ is its radius.
Now, using parallel axis theorem, the moment of inertia of the spherical shell about a tangential axis will be:
$\begin{align}
  & \dfrac{2}{3}M{{R}^{2}}+M{{R}^{2}} \\
 & \Rightarrow \dfrac{5}{3}M{{R}^{2}} \\
\end{align}$
The moment of inertia of a hemi-spherical shell about an axis passing through its centroid is:
$\dfrac{2}{3}M{{R}^{2}}$
Here, $M$ is the mass of the spherical shell and $R$ is its radius.
Now, using parallel axis theorem, the moment of inertia of the hemi-spherical shell about a tangential axis will be as follows:
$\begin{align}
  & \dfrac{2}{3}M{{R}^{2}}+M{{R}^{2}} \\
 & \Rightarrow \dfrac{5}{3}M{{R}^{2}} \\
\end{align}$
Thus, the moment of inertia of a spherical shell and a hemispherical shell of same mass and radius about a tangential axis, passing through $P$ will be the same.

Hence option $B$ is the correct option.

Note:
The parallel axis theorem helps us to find the moment of inertia of a body about an axis that is parallel to an axis about whom, the moment of inertia of that body is known to us. We used this theorem to solve the given question and found out the moment of inertia of the two bodies about a tangential axis.