
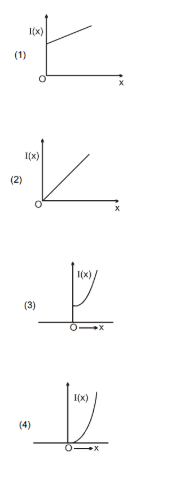
The moment of inertia of a solid sphere, about an axis parallel to its diameter and at a distance of x from it, is I(x)'. Which one of the graphs represents the variation of I(x) with x correctly?

Answer
583.2k+ views
Hint: Moment of inertia is the rotational analog of mass. Moment of inertia is measured by taking the second moment of mass with respect to distance from an axis. We have to find the equation of the graph I(x) v/s x and by comparing it with the general form of equations for conic sections we can find its shape (I.e. whether it is linear, parabolic etc.). Once the equation is known we can find the shape of the graph.
Formula used:
${I_{CM}} = \dfrac{2}{5}M{R^2}$ , where ${I_{CM}}$ is the moment of inertia of the solid sphere having radius $R$ about an axis parallel to the center of gravity.
$I = {I_{CM}} + M{X^2}$, where $I$ is the moment of inertia about axis passing through $O$, where ${I_{CM}}$ is the moment of inertia of the solid sphere having radius $R$ about an axis parallel to the center of gravity, $M$ is the mass of the body and $X$ is the distance between the axes.
Complete step by step answer:
Moment of inertia of the solid sphere about an axis parallel to its diameter and at a distance of x from it can be found out by using parallel axis theorem.
${I_{CM}} = \dfrac{2}{5}M{R^2}$ , where ${I_{CM}}$ is the moment of inertia of the solid sphere having radius $R$ about an axis parallel to the center of gravity. The distance between both the axes varies with respect to $x$ substituting these in the equation $I = {I_{CM}} + M{X^2}$, we get the moment of inertia of the solid sphere as with change in $x$.
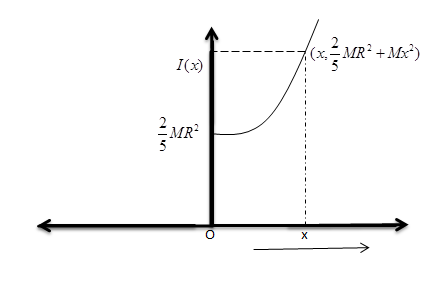
$I(x) = \dfrac{2}{5}M{R^2} + M{x^2}$
This is in the form of $y = 4a{x^2} + c$, where c is a constant and $4a$ represents the length of the latus rectum. This represents a parabola with $a = \dfrac{M}{4}$ and $c = \dfrac{2}{5}M{R^2}$.
Therefore (3) is the correct option.
Additional Information:
Parallel Axis Theorem: The moment of inertia of a body about any axis is equal to the sum of its moment of inertia about a parallel axis through its center of gravity and the product of the mass of the body and the square of the distance between the two axes.
Perpendicular Axis theorem: The moment of inertia of a plane laminar body about an axis perpendicular to the plane is equal to the sum of the moments of inertia about two mutually perpendicular axes in the plane of the lamina such that the three mutually perpendicular axes have a common point of intersection.
Note: When the value of x is zero, the moment of inertia of the solid sphere $I(x)$ is equal to ${I_{CM}}$.
Using $I(x) = \dfrac{2}{5}M{R^2} + M{x^2}$ also we can find that at $x = 0$, ${I_{CM}} = \dfrac{2}{5}M{R^2}$. Therefore the graph does not pass through the origin. Also note that the moment of inertia of an object cannot be zero.
Formula used:
${I_{CM}} = \dfrac{2}{5}M{R^2}$ , where ${I_{CM}}$ is the moment of inertia of the solid sphere having radius $R$ about an axis parallel to the center of gravity.
$I = {I_{CM}} + M{X^2}$, where $I$ is the moment of inertia about axis passing through $O$, where ${I_{CM}}$ is the moment of inertia of the solid sphere having radius $R$ about an axis parallel to the center of gravity, $M$ is the mass of the body and $X$ is the distance between the axes.
Complete step by step answer:
Moment of inertia of the solid sphere about an axis parallel to its diameter and at a distance of x from it can be found out by using parallel axis theorem.
${I_{CM}} = \dfrac{2}{5}M{R^2}$ , where ${I_{CM}}$ is the moment of inertia of the solid sphere having radius $R$ about an axis parallel to the center of gravity. The distance between both the axes varies with respect to $x$ substituting these in the equation $I = {I_{CM}} + M{X^2}$, we get the moment of inertia of the solid sphere as with change in $x$.

$I(x) = \dfrac{2}{5}M{R^2} + M{x^2}$
This is in the form of $y = 4a{x^2} + c$, where c is a constant and $4a$ represents the length of the latus rectum. This represents a parabola with $a = \dfrac{M}{4}$ and $c = \dfrac{2}{5}M{R^2}$.
Therefore (3) is the correct option.
Additional Information:
Parallel Axis Theorem: The moment of inertia of a body about any axis is equal to the sum of its moment of inertia about a parallel axis through its center of gravity and the product of the mass of the body and the square of the distance between the two axes.
Perpendicular Axis theorem: The moment of inertia of a plane laminar body about an axis perpendicular to the plane is equal to the sum of the moments of inertia about two mutually perpendicular axes in the plane of the lamina such that the three mutually perpendicular axes have a common point of intersection.
Note: When the value of x is zero, the moment of inertia of the solid sphere $I(x)$ is equal to ${I_{CM}}$.
Using $I(x) = \dfrac{2}{5}M{R^2} + M{x^2}$ also we can find that at $x = 0$, ${I_{CM}} = \dfrac{2}{5}M{R^2}$. Therefore the graph does not pass through the origin. Also note that the moment of inertia of an object cannot be zero.
Recently Updated Pages
Master Class 11 Chemistry: Engaging Questions & Answers for Success

Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




