Question

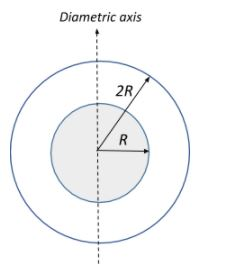
The moment of inertia of a hollow sphere (mass M) of inner radius R and outer radius 2R, having material of uniform density, about a diametric axis is:
A. $\dfrac{31MR^2}{14}$
B. $\dfrac{43MR^2}{90}$
C. $\dfrac{19MR^2}{80}$
D. None

Answer 1

Hint: Recall that a hollow sphere does not enclose any mass within its boundary. Therefore, the only source of mass which contributes to the moment of inertia of such a sphere is the mass enclosed between the inner and outer radius of the sphere. In such a case, assuming that the density of the sphere remains uniform throughout this enclosed region, first determine an expression for the density of this region taking it as mass per volume of the region, and then determine the mass of the enclosed region by taking the difference in the mass encompassed by the two radii.
From this, the moment of inertia can be determined by taking the difference of the moment of inertia about the diametric axis between the inner and outer radii and corresponding masses to ultimately arrive at the required solution.

Formula used:
Moment of inertia of hollow spherical shell $I = I_{R_2} -I_{R_1}$

Complete step-by-step answer:
The moment of inertia of the hollow sphere comes from the region enclosed between the inner and outer radius of the sphere, since all mass of the sphere lies in this enclosed region.
$I = I_{2R} -I_{R} = \dfrac{1}{2}M_{2R}(2R)^2 - \dfrac{1}{2}M_{R}R^2$
We now need to find $M_{2R}$ and $M_R$.
Let us assume that the density of the sphere over this region between R and 2R is uniform, and can be given as:
$\rho = \dfrac{M}{V}$, where M is the mass of the enclosed region and V is the volume of this enclosed region.
$\rho = \dfrac{M}{V_{2R} – V_{R}} = \dfrac{M}{\left(\dfrac{4}{3}\pi(2R)^3\right)- \left(\dfrac{4}{3}\pi(R)^3\right)}$
$\Rightarrow \rho = \dfrac{M}{\left(\dfrac{32\pi R^3- 4\pi R^3}{3}\right)} = \dfrac{3M}{28\pi R^3} $
Now, $M_{2R}$ can be calculated as:
$M_{2R} = \rho \times V_{2R} = \dfrac{3M}{28\pi R^3}. \left(\dfrac{4}{3}\pi(2R)^3\right) = \dfrac{3}{28}.\dfrac{4}{3}.8M$
$\Rightarrow M_{2R} = \dfrac{8}{7}M$

Similarly,
$M_{R} = \rho \times V_{R} = \dfrac{3M}{28\pi R^3}. \left(\dfrac{4}{3}\pi(R)^3\right) = \dfrac{3}{28}.\dfrac{4}{3}.M$
$\Rightarrow M_{R} = \dfrac{1}{7}M$
Therefore, from the equation for the moment of inertia:
$I = \dfrac{1}{2}M_{2R}(2R)^2 - \dfrac{1}{2}M_{R}R^2$
$\Rightarrow I = \dfrac{1}{2}.\dfrac{8}{7}M.(4R^2) - \dfrac{1}{2}.\dfrac{1}{7}M.(R^2)$
$\Rightarrow I = \dfrac{32MR^2 – 1MR^2}{14} = \dfrac{31MR^2}{14}$
Therefore, the correct choice would be: A. $\dfrac{34MR^2}{14}$

So, the correct answer is “Option A”.

Note: Always remember that the moment of inertia does not only depend on the shape of the object but also on the position and orientation of the axis of rotation and the distribution of mass of the body about the axis of rotation. If our spherical shell was variably dense across the diametric axis, then we would have to find the mass of the sphere across every differently dense region and cumulatively add them up together to get the mass of the enclosed region.