Question

The moment of inertia of a disc of radius $ 0.5 $ m about its geometric axis is $ 2kg \cdot {m^2} $ . If a string is tied to its circumference and a force of 10 N is applied, what is the value of torque with respect to this axis?

Answer 1

Hint
Torque is the force that is responsible for making an object rotate about an axis. Depending on the position of the axis and the distance of the force acting, the value of torque may vary.
Formula used: $ T = Fr $ where $ T $ is the torque acting on the body, $ F $ is the force applied and $ r $ is the distance between the point of application of force and the axis of torque. The SI unit is Nm.

Complete step by step answer
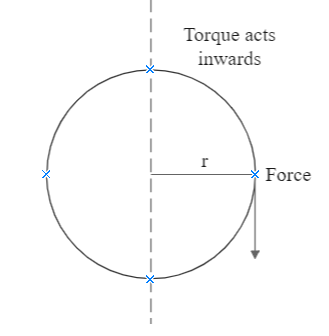
In this question, we are provided with a circular disc. A string is attached on the circumference of the disk, and through it some force is applied. Naturally, this tangential action would cause the disk to rotate. We are required to find the torque when the disc starts rotating about its central axis. The details provided to us include:
Radius of the disc is $ r = 0.5 $ m
Force acting is $ F = 10{\text{ N}} $
Moment of inertia is $ I = 2kg \cdot {m^2} $
We know that the torque can be calculated as:
 $ T = Fr $

Substituting the given values in the above equation, we get:
 $ T = 10 \times 0.5 $
 $ \Rightarrow T = 5{\text{ Nm}} $
Hence, the amount of torque acting along the central axis of the provided disc is 5 Nm.

Note
Moment of inertia is helpful in determining the angular momentum of a rotating body having some mass. In this question, we did not need to use this property because the axis about which the moment of inertia was given coincided with the axis about which we were required to find the torque.