Question

The moment of inertia of a circular ring of mass M and radius R about diameter is
\[\begin{align}
  & A)\dfrac{1}{2}M{{R}^{2}} \\
 & B)\dfrac{3}{2}M{{R}^{2}} \\
 & C)\dfrac{M{{R}^{2}}}{2} \\
 & D)2M{{R}^{2}} \\
\end{align}\]

Answer 1

Hint: First we calculate the moment of inertia of circular ring of radius R and mass M about is centre perpendicular to the plane of ring by taking a small element and then calculate the effective mass of that portion and then integrate it for whole ring and then we apply theorem of perpendicular axis for calculating the moment of inertia about diameter.

Complete answer:
Consider a ring of mass M and Radius R passing through an axis AB .
AB is the axis of rotation passing through point O and perpendicular to the plane of ring.
First we calculate moment of inertia about axis passing through centre and perpendicular to plane of ring
Length of the ring\[=2\pi R\].
The mass M is distributed over the length ring. So to calculate moment of inertia we will consider a small element \[dx\]of mass\[dm\].
We will calculate the value of mass\[dm\]by applying a unitary method.

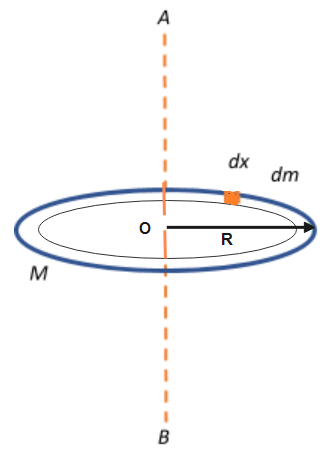
Since, Mass of Whole ring of Length \[2\pi R\]\[=M\]
Mass of Unit length of ring = \[\dfrac{M}{2\pi R}\]
Mass of length dx of ring = \[\dfrac{M}{2\pi R}\times dx\]
so, \[dm=\dfrac{Mdx}{2\pi R}\]\[(Equation1)\]
so, moment of inertia of elementary portion of the ring about the axis AB is expressed as -
\[dI=dm{{R}^{2}}\]\[(Equation2)\]
Then moment of inertia of whole ring about the axis AB is calculated as -
\[\Rightarrow \]\[I=\int{dI}\]
Put the value of dI from equation 2 in above equation , we get
\[I=\int{\left( dm{{R}^{2}} \right)}\]
Put value of dm from equation 1
\[\Rightarrow \]\[I=\int{\dfrac{Mdx}{2\pi R}{{R}^{2}}}\]
\[\Rightarrow \]\[I=\dfrac{MR}{2\pi }\int{dx}\]\[(Equation3)\]
dx is the small portion of the ring when we integrate this small portion then we get the length of the whole ring.
 \[dx=2\pi R\]
Put this value of dx in equation 3
\[\Rightarrow \]\[I=\dfrac{MR}{2\pi }\times 2\pi R\]
\[\therefore \]\[I=M{{R}^{2}}\]
So inertia about the axis at the centre of the ring and perpendicular to its plane is given by\[M{{R}^{2}}\].
Now we have to calculate moment of inertia about diameter so we theorem of perpendicular axis

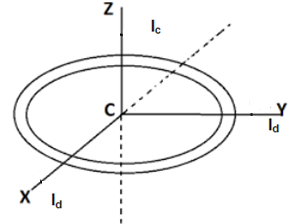
According to the theorem of perpendicular axis, Moment of Inertia about any axis is sum of moment of inertia of the remaining two mutually perpendicular axes. According to figure, \[{{I}_{Z}}={{I}_{X}}+{{I}_{Y}}\]
Moment of inertia along Z axis is the axis passing through centre, so moment of inertia along z axis is represented as \[{{I}_{Z}}=M{{R}^{2}}\]
Moment of inertia along diameter is given by\[{{I}_{y}}\And {{I}_{x}}\].
Apply theorem of perpendicular axis;
 \[\Rightarrow \]\[{{I}_{z}}={{I}_{d}}+{{I}_{d}}\]
\[\Rightarrow \]\[{{I}_{d}}=\dfrac{1}{2}{{I}_{z}}\]
Put the value of \[{{I}_{z}}\] in this equation,
\[\therefore \] \[{{I}_{d}}\] = \[ \dfrac{1}{2}M{{R}^{2}}\]

Correct options are A and C.

Note:
Moment of inertia of the ring at the centre axis perpendicular to the plane is equal to the moment of inertia of hollow cylinder because hollow cylinder is also acting like a ring of large thickness and formula of inertia does not contain the thickness of ring. So a hollow cylinder has the same moment of inertia about the central axis.