Question

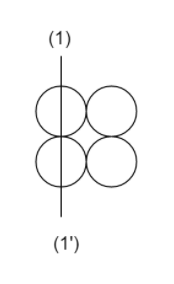
The moment of inertia about the axis $1 - 1'$ for system of solid sphere shown will be $(M = 1Kg, R = 1m)$

A. $48Kg.{m^2}$
B. $60Kg.{m^2}$
C. $70Kg.{m^2}$
D. $50Kg.{m^2}$

Answer 1

Hint: Moment of inertia depends upon the centre of mass. We need to find the moment of inertia of the respective spheres, then putting the values of mass and radius, we can find the moment of inertia of the combined system.

Complete step by step answer:

We know, mathematically, we can write the moment of inertia as the ratio of angular momentum and angular velocity around the principal axis.
$I = \dfrac{L}{\omega }$
Here, $L$ is the angular momentum and $\omega$ is the angular velocity and $I$ is the moment of inertia.
In case of moment of inertia of the simple pendulum, it depends on mass $m$ and radius $r$. This radius is calculated from the pivot point.
$I = m{R^2}$
In the case of a sphere, we know the moment of inertia is $m{R^2}$. This radius is calculated from the centre.
In the figure, sphere $B$ and $D$ Lies away from the centre.
Therefore, ${R_B} = {R_D} = R + R = 2R$
We know, the Parallel axis theorem gives the formula for calculating moment of inertia of objects that lie away from the centre.
 The moment of inertia is given by: $I = {I_{CM}} + m{d^2}$
Here, ${I_{CM}}$ is the moment of inertia at the centre of the axis and $dcm$ is the displaced distance.
Therefore, moment of inertia of the sphere $B$ is equal to, moment of inertia of the sphere $D$:
${I_B} = \dfrac{2}{5}m{R^2} + m{(2R)^2}$
Now, the moment of inertia of the combined system is ${I_A} + {I_B} + {I_C} + {I_D}$
Putting the values:
$I = \dfrac{2}{5}m{R^2} + \dfrac{2}{5}m{R^2} + m{(2R)^2} + \dfrac{2}{5}m{R^2} + \dfrac{2}{5}m{R^2} + m{(2R)^2}$
We know, $m = 1Kg$ and $R = 1m$
Thus, we obtain:
$I = 48Kg.{m^2}$

Hence, the correct answer is option (A).

Note: We have two theorems governing the actions of rotational motion. One is the parallel axis theorem and the other is the perpendicular axis theorem. Parallel axis theorem gives the moment of inertia of objects displaced by a certain distance from the axis. Since the spheres are displaced from the axis, we have used the parallel axis theorem.