
The mirror image of the curve
A.
B.
C.
D.
Answer
486.6k+ views
Hint: First of all find the locus represented by the curve. And then we will find the mirror image along the given line. We know that a complex number is
Complete step-by-step answer:
Given that,
So write the curve given above in complex number form as
Taking i common in numerator, and writing real and imaginary part as in complex number
Now to simplify the terms we will multiply numerator and denominator by
Now multiply the terms in numerator and denominator will be
Since
Multiplying the terms in numerators and separating the real and imaginary parts
The terms xy cancels here and we get
Now here we separated the real and imaginary terms.
Given that
In this case real and imaginary parts are the same. So equating them,
Cancelling the denominators from both the sides
Adding x and y terms,
Now if we observe this is the locus of a circle with center
It can be plotted as ,
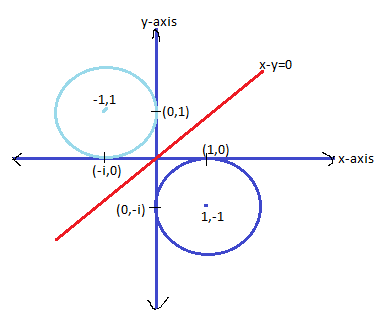
Now since the locus of light blue circle is the mirror image of the curve. Thus the curve is given as
Hence option C is the correct answer.
Note: Students generally make mistakes when we simplify the fraction with the help of complex conjugate of term in denominator. So take the simplification term carefully. And the mirror image of the curve is along the line x=y so draw that line to get an exact idea of the mirror locus.
Complete step-by-step answer:
Given that,
So write the curve given above in complex number form as
Taking i common in numerator, and writing real and imaginary part as in complex number
Now to simplify the terms we will multiply numerator and denominator by
Now multiply the terms in numerator and denominator will be
Since
Multiplying the terms in numerators and separating the real and imaginary parts
The terms xy cancels here and we get
Now here we separated the real and imaginary terms.
Given that
In this case real and imaginary parts are the same. So equating them,
Cancelling the denominators from both the sides
Adding x and y terms,
Now if we observe this is the locus of a circle with center
It can be plotted as ,

Now since the locus of light blue circle is the mirror image of the curve. Thus the curve is given as
Hence option C is the correct answer.
Note: Students generally make mistakes when we simplify the fraction with the help of complex conjugate of term in denominator. So take the simplification term carefully. And the mirror image of the curve is along the line x=y so draw that line to get an exact idea of the mirror locus.
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

The reason why India adopted the policy of nonalignment class 11 social science CBSE

How much is 23 kg in pounds class 11 chemistry CBSE

The plastids which are coloured green and colourless class 11 biology CBSE




