Question

The minimum distance between the circle ${x^2} + {y^2} = 9$ and the curve $2{x^2} + 10{y^2} + 6xy = 1$ is?
A. $2\sqrt 2 $
B. $2$
C. $3 - \sqrt 2 $
D. $3 - \dfrac{1}{{\sqrt {11} }}$

Answer 1

Hint: We are given with a circle with center origin and a curve. We can prove that the normal of the curve will pass through the origin. Then we find the maximum distance from the origin to the curve. We will get the required answer after subtracting this distance from the radius.

Complete step by step answer:

We can plot the graph for better understanding of the problem.

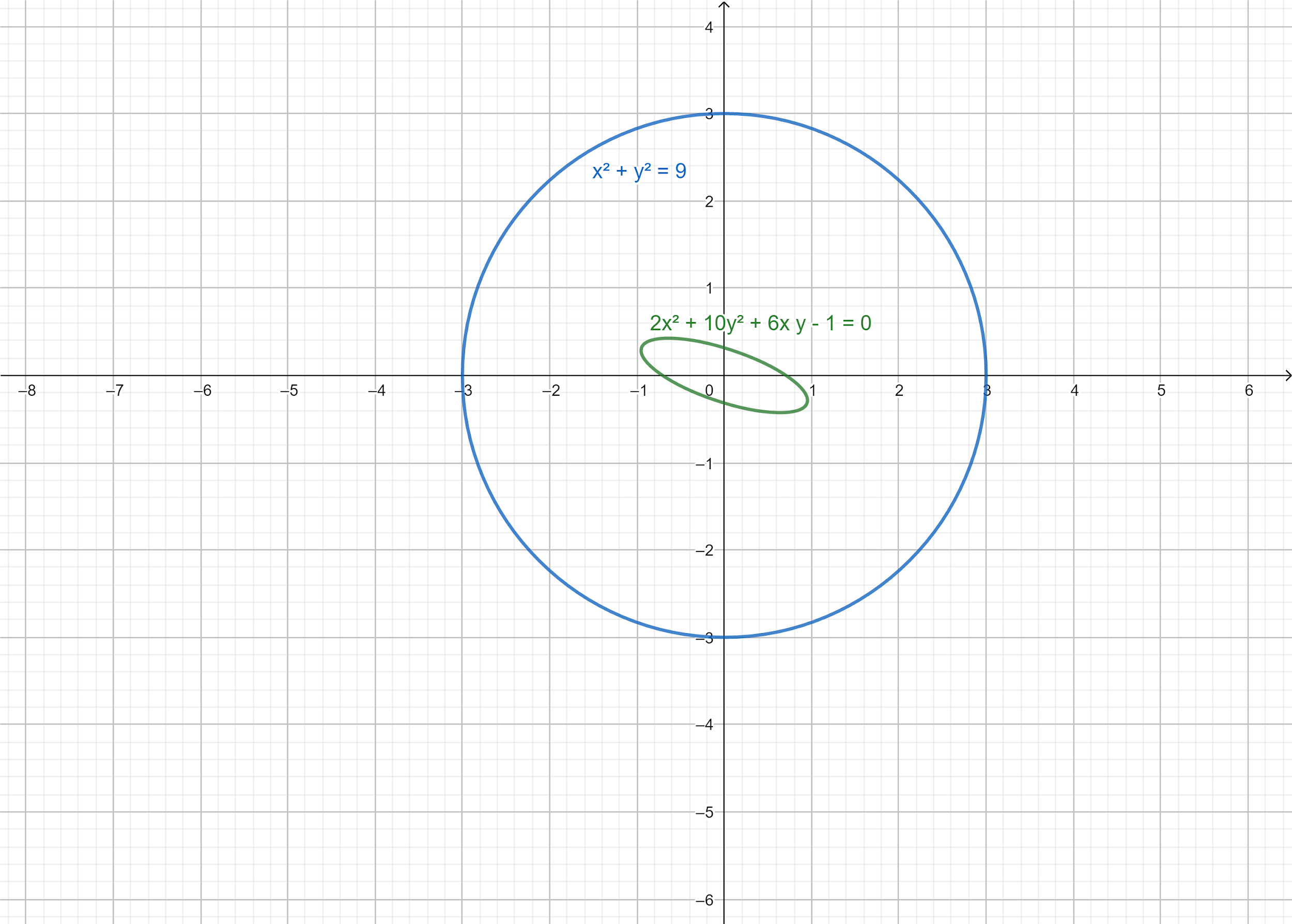
We have equation of a circle, ${x^2} + {y^2} = 9$.
Comparing with the standard equation of the circle ${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}$
From the equation, the center of circle is (0,0) and radius is $r = 3$.
We have equation of the curve, $g\left( {x,y} \right) = 2{x^2} + 10{y^2} + 6xy = 1$ … (1)
To find the center of the curve, we can find the normal to the curve.
It is given by, \[\nabla g\left( {x,y} \right) = 0\]
$ \Rightarrow {g_x} = 0$ and ${g_y} = 0$
We can partially (1) differentiate w.r.t x, we get,
${g_x} = 4x + 6y$
${g_x} = 0$
$ \Rightarrow 4x + 6y = 0$… (2)
We can partially differentiate (1) w.r.t y, we get,
${g_y} = 20y + 6x$
\[{g_y} = 0\]
$ \Rightarrow 20y + 6x = 0$… (3)
The point where the normal meet will be center of the curve.
Solving (2) and (3), we get,
Subtracting 4 times equation (3) from 6 times equation (2), we get
$
  {\text{ }}24x + 36y = 0 \\
   - \left( {24x + 80y = 0} \right) \\
  {\text{ }}\overline {0x + 116y = 0} \\
 $
We get,\[y = 0\]. Now put this result in equation (1), we get \[x = 0\]
 \[\left( {x,y} \right) = \left( {0,0} \right)\]
Therefore, the center of the curve is also $\left( {0,0} \right)$.
From the figure we can understand that the distance between the circle and curve is radius of the circle minus the distance from origin to the curve. As the radius of the circle is constant, the required distance will be minimum when the distance from the curve to the origin is maximum.
The distance from any point \[\left( {x,y} \right)\]on the curve to origin is given by,
$
  d = \sqrt {{{\left( {x - 0} \right)}^2} + {{\left( {y - 0} \right)}^2}} \\
   = \sqrt {{x^2} + {y^2}} \\
 $
\[ \Rightarrow {d^2} = {x^2} + {y^2}\]
d is maximum when \[{d^2}\] is maximum.
For maximizing, we use Lagrange multipliers.
We need to maximize $f(x,y) = {x^2} + {y^2}$ over the constrain $g\left( {x,y} \right) = 2{x^2} + 10{y^2} + 6xy - 1$.
By Lagrange multiplier,
\[\nabla f\left( {x,y} \right) = \lambda \times \nabla g\left( {x,y} \right)\]
Taking partial derivative of f w.r.t x
${f_x} = 2x$
Taking partial derivative of f w.r.t y
${f_y} = 2y$
Taking partial derivative of g w.r.t x
${g_x} = 4x + 6y$
Taking partial derivative of g w.r.t y
${g_y} = 20y + 6x$
Applying Lagrange’s conditions, we get,
$
  {f_x} = \lambda {g_x} \\
  2x = \lambda \left( {4x + 6y} \right) \\
 $
On simplifying we get,
\[ \Rightarrow x = \lambda \left( {2x + 3y} \right)\]
\[ \Rightarrow \lambda = \dfrac{x}{{\left( {2x + 3y} \right)}}\] … (4)
$
  {f_y} = \lambda {g_y} \\
  2y = \lambda \left( {20y + 6x} \right) \\
 $
On simplifying we get,
$ \Rightarrow y = \lambda \left( {10y + 3x} \right)$
$ \Rightarrow \lambda = \dfrac{y}{{\left( {10y + 3x} \right)}}$ … (5)
On Comparing equations (4) and (5), we get,
$\dfrac{x}{{\left( {2x + 3y} \right)}} = \dfrac{y}{{\left( {10y + 3x} \right)}}$
On Cross multiplying, we get,
$
  \left( {10y + 3x} \right)x = \left( {2x + 3y} \right)y \\
   \Rightarrow 10xy + 3{x^2} = 2xy + 3{y^2} \\
 $
On simplifying we get,
$ \Rightarrow 3{x^2} + 8xy - 3{y^2} = 0$
Making complete square,
${\left( {\sqrt 3 x} \right)^2} + 2 \times \left( {\sqrt 3 x} \right) \times \left( {\dfrac{4}{{\sqrt 3 }}y} \right) + {\left( {\dfrac{4}{{\sqrt 3 }}y} \right)^2} - {\left( {\dfrac{4}{{\sqrt 3 }}y} \right)^2} - 3{y^2} = 0$
$ \Rightarrow {\left( {\sqrt 3 x} \right)^2} + 2 \times \left( {\sqrt 3 x} \right) \times \left( {\dfrac{4}{{\sqrt 3 }}y} \right) + {\left( {\dfrac{4}{{\sqrt 3 }}y} \right)^2} = \dfrac{{16}}{3}{y^2} + 3{y^2}$
\[ \Rightarrow {\left( {\sqrt 3 x + \dfrac{4}{{\sqrt 3 }}y} \right)^2} = \left( {\dfrac{{16 + 9}}{3}} \right){y^2} = \dfrac{{25}}{3}{y^2}\]
Taking square root, we get,
\[ \Rightarrow \sqrt 3 x + \dfrac{4}{{\sqrt 3 }}y = \pm \sqrt {\dfrac{{25}}{3}{y^2}} = \pm \dfrac{5}{{\sqrt 3 }}y\]
\[
   \Rightarrow \sqrt 3 x = - \dfrac{4}{{\sqrt 3 }}y \pm \dfrac{5}{{\sqrt 3 }}y \\
   \Rightarrow x = - \dfrac{4}{3}y \pm \dfrac{5}{3}y \\
   \Rightarrow x = \left( { - 4 \pm 5} \right)\dfrac{y}{3} \\
 \]
$ \Rightarrow x = \dfrac{1}{3}y, - 3y$
Now we need to plug the above equation in $g\left( {x,y} \right) = 0$.
For $x = \dfrac{1}{3}y$, ${x^2} = \dfrac{{{y^2}}}{9}$
$g\left( {x,y} \right) = 2{x^2} + 10{y^2} + 6xy - 1$
$ \Rightarrow 2\dfrac{{{y^2}}}{9} + 10{y^2} + 6y\dfrac{y}{3} - 1 = 0$
Multiplying throughout with 9, we get,
$ \Rightarrow 2{y^2} + 90{y^2} + 18{y^2} - 9 = 0$
$ \Rightarrow 110{y^2} = 9$
\[ \Rightarrow {y^2} = \dfrac{9}{{110}}\]
Taking square root we get,
$ \Rightarrow y = \pm \sqrt {\dfrac{9}{{110}}} = \pm \dfrac{3}{{\sqrt {110} }}$
$ \Rightarrow x = \dfrac{1}{3}y = \pm \dfrac{1}{{\sqrt {110} }}$
For $x = - 3y$, ${x^2} = 9{y^2}$
$g\left( {x,y} \right) = 2{x^2} + 10{y^2} + 6xy - 1$
$2 \times 9{y^2} + 10{y^2} + 6y\left( { - 3y} \right) - 1 = 0$
$ \Rightarrow 18{y^2} + 10{y^2} - 18{y^2} = 1$
$ \Rightarrow 10{y^2} = 1$
$ \Rightarrow {y^2} = \dfrac{1}{{10}}$
Taking square root, we get,
$ \Rightarrow y = \pm \sqrt {\dfrac{1}{{10}}} = \pm \dfrac{1}{{\sqrt {10} }}$
\[ \Rightarrow x = - 3y = \mp \dfrac{3}{{\sqrt {10} }}\]
Now we have critical points, $\left( { \pm \dfrac{1}{{\sqrt {110} }}, \pm \dfrac{3}{{\sqrt {110} }}} \right)$and $\left( { \pm \dfrac{3}{{\sqrt {10} }}, \mp \dfrac{1}{{\sqrt {10} }}} \right)$
Taking the 1^st set of points,
${x^2} = \dfrac{1}{{110}}$
${y^2} = \dfrac{9}{{110}}$
\[ \Rightarrow {d^2} = {x^2} + {y^2} = \dfrac{1}{{110}} + \dfrac{9}{{110}} = \dfrac{{10}}{{110}} = \dfrac{1}{{11}}\]
Taking the 2^nd points, we get,
${x^2} = \dfrac{1}{{10}}$
${y^2} = \dfrac{9}{{10}}$
\[ \Rightarrow {d^2} = {x^2} + {y^2} = \dfrac{1}{{10}} + \dfrac{9}{{10}} = \dfrac{{10}}{{10}} = 1\]
Maximum value of ${{\text{d}}^{\text{2}}}$is equal to 1. So, $d = \sqrt 1 = 1$ unit.
From the figure, minimum distance from the curve to the circle is given by,
${{\text{D}}_{\text{m}}}{\text{ = r - d = 3 - 1 = 2}}$ units.
Therefore, the correct answer is option B.

Note: We must plot the curves to get an idea of how to solve the question. Lagrange’s multipliers are used to minimize or maximize values of function with constrains. Here we have the square of the distance as the function to maximized and the point must lie on the curve, i.e. the point must satisfy the equation of the curve is the constraining function. We are using the concepts of gradients and partial differentiation for finding the normal and in Lagrange multipliers. While taking partial derivatives with respect to one variable we consider other variables as constants proceed with differentiation. In this problem we must take care while taking square roots that they can be both positive and negative. We must be very careful as there are a lot of calculations involved.