Question

The minimum acceleration with which a fireman can slide down a rope of breaking strength two=third of his weight is,
A. Zero
B. G/3
C. 3g
D. G

Answer 1

Hint: Here we will be applying the concept of apparent weight of a man in a lift or elevator.
$R = mg$
${R_2} = mg - ma = m(g - a)$
Where m is the mass of the system, g is acceleration due to gravity, a is acceleration of a lift or elevator and R is the reaction force.

Complete step-by-step answer:
Consider a person of mass ‘m’ standing on a weighing machine placed in an elevator or lift. The actual weight of the person =mg. This acts on the weighing machine which offers a reaction R given by the reading of the weighing machine. This reaction exerted by the surface of contact on the person is the apparent weight of the person.
In this question, the given case is similar to when the lift or elevator is moving downwards with acceleration ‘a’ or moving upwards with retardation ‘a’.

This is free body diagram (F.B.D)of a lift:

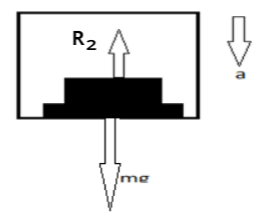
A lift is moving downward with acceleration a, then weight of the person mg is acting downward towards the centre of the earth. And there is normal force perpendicular to the surface r2. Now using vector addition,
Then, ${R_2}{\text{ less than mg}}$. Because weight of the body as well as acceleration acting downwards during motion. Therefore, when the elevator is moving downwards the apparent weight of the person decreases.
Now, from the above figure, $mg - {R_2} = ma$
$mg - {R_2}$ is obtained like, mg is more in magnitude acting downward and reaction force ${R_2}$ less in magnitude acting upwards. Here mg and ${R_2}$ are in the opposite direction therefore, there is subtraction of those two. And ma is the external force, because of acceleration.
${R_2} = mg - ma = m(g - a)$
Given, a fireman slides down with some acceleration then his apparent weight decreases. Especially in this question it is given that rope can bear only $\dfrac{2}{3}{\text{rd}}$ of the fireman’s weight. Let ’a’ be the minimum acceleration then,
That is $T = \dfrac{2}{3}mg$ (given in the question)
Then, $\dfrac{2}{3}mg = m(g - a)$
$a = g - \dfrac{{2g}}{3} = \dfrac{g}{3}$
Therefore, the correct answer is option (B).

Note: While solving these types of problems, observe that, a lift or elevator or a person sliding through rope is moving upward or downward or at rest. Then start applying formulas using a free body diagram.