Question

The medians of a right-angled triangle which are drawn from the vertices of the acute angles are 6 cm and 8 cm, then the length of the hypotenuse is:
(a) \[2\sqrt{5}\]cm
(b) \[3\sqrt{5}\]cm
(c) \[4\sqrt{5}\]cm
(d) \[5\sqrt{5}\]cm

Answer 1

Hint: In this question, we first need to draw the diagram so that we get a clear picture of what we have to find. Now, as the median divides the side into two equal halves we get the respective relations. Then consider the triangles with respect to the medians and apply the Pythagoras theorem given by square of hypotenuse is equal to sum of the squares of the other two sides. In triangle ABC right angled at B it is given by \[A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}}\]and then simply further to get the result.

Complete step-by-step answer:
Now, let us assume the right angled triangle as ABC right angled at B and the medians as AE and CD
Given in the question that \[AE=6,CD=8\]
Let us draw the diagram with the above conditions

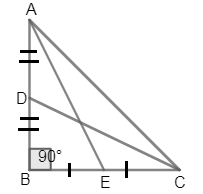
As AE and CD are the medians of the triangle they divide the corresponding side into two equal halves so that we get,
Now, on considering the median AE and the corresponding side we get,
\[\Rightarrow BE=EC=\dfrac{1}{2}BC\]
Now, on considering the median CD and the side AB we get,
\[\Rightarrow AD=DB=\dfrac{1}{2}AB\]
Let us now consider the triangle \[\vartriangle ABE\]
Now, on applying the Pythagoras theorem to this triangle we get,
\[\Rightarrow A{{B}^{2}}+B{{E}^{2}}=A{{E}^{2}}\]
Now, on substituting the respective values we get,
\[\Rightarrow A{{B}^{2}}+{{\left( \dfrac{1}{2}BC \right)}^{2}}={{6}^{2}}\]
Now, on further simplification we get,
\[\Rightarrow A{{B}^{2}}+\dfrac{1}{4}B{{C}^{2}}=36.........\left( 1 \right)\]
Let us now consider the triangle \[\vartriangle CBD\]
Now, on applying the Pythagoras theorem to this triangle we get,
\[\Rightarrow B{{C}^{2}}+D{{B}^{2}}=C{{D}^{2}}\]
Now, on substituting the respective values we get,
\[\Rightarrow B{{C}^{2}}+{{\left( \dfrac{1}{2}AB \right)}^{2}}={{8}^{2}}\]
Now, on further simplification we get,
\[\Rightarrow B{{C}^{2}}+\dfrac{1}{4}A{{B}^{2}}=64........\left( 2 \right)\]
Let us now add the equations (1) and (2) to simplify further
\[\Rightarrow A{{B}^{2}}+\dfrac{1}{4}B{{C}^{2}}+B{{C}^{2}}+\dfrac{1}{4}A{{B}^{2}}=36+64\]
Now, this can be further written as
\[\Rightarrow \dfrac{5}{4}A{{B}^{2}}+\dfrac{5}{4}B{{C}^{2}}=100\]
Now, on rearranging the terms and further simplification we get,
\[\Rightarrow A{{B}^{2}}+B{{C}^{2}}=\dfrac{4\times 100}{5}\]
As we already know from the \[\vartriangle ABC\]that
\[A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}}\]
Now, on substituting this in the above equation and simplifying further we get,
\[\Rightarrow A{{C}^{2}}=80\]
Let us now apply the square root on both sides,
\[\Rightarrow \sqrt{A{{C}^{2}}}=\sqrt{80}\]
Now, on further simplification we get,
\[\therefore AC=4\sqrt{5}\]
Hence, the correct option is (c).

Note:
Instead of considering the two triangles we can directly solve it by substituting the relation obtained between the medians and sides in the Pythagoras theorem applied on the triangle ABC and simplify further to get the result.
It is important to note that we need to substitute the corresponding values and the relations because neglecting any of the terms and substituting incorrectly changes the complete result.