Question

The maximum tension in the string of an oscillating pendulum is double of the minimum tension. Find the angular amplitude.

Answer 1

Hint: Use the law of conservation of energy at extreme position and mean position of swing of pendulum to determine the velocity at mean position. The centripetal force is related to the velocity of the body. The tension in the string at these two positions is the sum of force due to weight and centrifugal force on the pendulum.

Formula used:
\[K.E. = \dfrac{1}{2}m{v^2}\]
\[P.E. = mgh\]

Here, m is the mass, v is the velocity, g is the acceleration due to gravity and h is the height above the ground.

Complete step by step answer:
The tension in the string of oscillating pendulum is maximum at the mean position and minimum at the extreme position. The tension in the oscillating pendulum is due to the sum of weight of the pendulum and the centripetal force on the mass of the pendulum.

We can draw the free body diagram of the forces acting on the pendulum at its mean position and extreme position as follows,

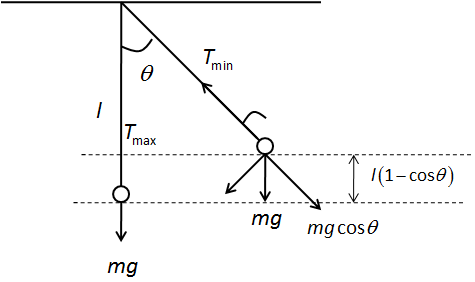
We can apply law of conservation of energy at extreme position and mean position as follows,
\[\dfrac{1}{2}m{v^2} = mgl\left( {1 - \cos \theta } \right)\]
\[ \Rightarrow {v^2} = 2gl\left( {1 - \cos \theta } \right)\]
Here, m is the mass of the pendulum, v is the velocity at mean position and l is the length of the string.

The centripetal force on the pendulum is,
\[{F_c} = \dfrac{{m{v^2}}}{l}\]

The tension in the string balances the centripetal force. Therefore, the net force in vertical direction at mean position is,
\[{T_{\max }} = mg + \dfrac{{m{v^2}}}{l}\]

Substitute expression for \[{v^2}\] in the above equation.
 \[{T_{\max }} = mg + \dfrac{{m\left( {2gl\left( {1 - \cos \theta } \right)} \right)}}{l}\]
\[{T_{\max }} = mg + 2mg\left( {1 - \cos \theta } \right)\] …… (1)

The net force in the string at extreme position is,
\[{T_{\min }} = mg\cos \theta \]

We have given,
\[{T_{\max }} = 2{T_{\min }}\]

Therefore,
 \[mg + 2mg\left( {1 - \cos \theta } \right) = 2mg\cos \theta \]
\[ \Rightarrow mg + 2mg - 2mg\cos \theta = 2mg\cos \theta \]
\[ \Rightarrow 3mg = 4mg\cos \theta \]
\[ \Rightarrow \cos \theta = \dfrac{3}{4}\]
\[ \Rightarrow \theta = {\cos ^{ - 1}}\left( {\dfrac{3}{4}} \right)\]

Therefore, the maximum amplitude of the pendulum is \[{\cos ^{ - 1}}\left( {\dfrac{3}{4}} \right)\].

Note:In this question, we have considered centrifugal force on the pendulum rather than the centripetal force in the string. The centrifugal force is along the string but in the opposite direction that is in the direction of weight of the pendulum. Therefore, we have taken the sum of forces and not the difference.