Question

The maximum shift of the center of mass system from its initial position is:
A. \[4m\]
B. \[2\sqrt 2 m\]
C. zero
D. \[4\sqrt 2 m\]

Answer 1

Hint:The shift in the center of masses of the system needs to be calculated based on the frame of reference of x-axis and y-axis. In order to find the maximum shift of the center of mass system, one needs to consider the subtraction of the initial position with the final position of the system.

Formula Used:
The position of center of mass of a system is given by:
\[\dfrac{{\sum {m_i}{x_i}}}{{\sum {m_i}}}\]

Complete step by step answer:
The center of mass of a rigid body is a fixed point. For bodies having regular symmetrical shapes and uniform distribution of mass, the center of mass system can easily be determined by the symmetry of the body. The center of mass of the system depends upon the masses of the constituent particles and their respective position vectors. It is independent of the forces that are acting on the system.

The position of center of mass of a system is given by:
\[\dfrac{{\sum {m_i}{x_i}}}{{\sum {m_i}}}\]
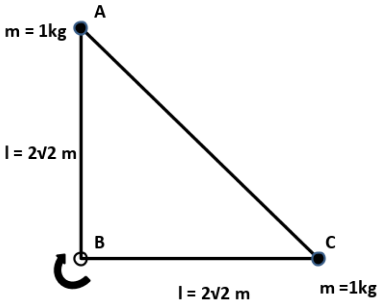
In the given figure, there are two masses of 1kg at length \[2\sqrt 2 \] m from the point B.
\[{x_{c.m}} = \dfrac{{(0 \times m) + (2\sqrt 2 \times m)}}{{m + m}} \\
\Rightarrow{x_{c.m}} = \dfrac{{(0 \times 1) + (2\sqrt 2 \times 1)}}{{1 + 1}} \\
\Rightarrow{x_{c.m}} = \dfrac{{2\sqrt 2 }}{2} = \sqrt 2 \hat i\]
\[\Rightarrow{y_{c.m}} = \dfrac{{(2\sqrt 2 \times m) + (0 \times m)}}{{m + m}}\\
\Rightarrow{y_{c.m}} = \dfrac{{(2\sqrt 2 \times 1) + (0 \times 1)}}{{1 + 1}} \\
\Rightarrow{y_{c.m}} = \dfrac{{2\sqrt 2 }}{2} \\
\Rightarrow{y_{c.m}} = \sqrt 2 \hat j\]
Therefore initial position of the system is: \[\sqrt 2 \hat i + \sqrt 2 \hat j\]

The final position will be: \[ = - \sqrt 2 \hat i + ( - \sqrt 2 \hat j)\]
Therefore, the maximum shift of the center of mass will be:
Final position – Initial position:
$- \sqrt 2 \hat i + ( - \sqrt 2 \hat j) - (\sqrt 2 \hat i + \sqrt 2 \hat j) \\
\Rightarrow - 2\sqrt 2 \hat i - 2\sqrt 2 \hat j \\$
The magnitude will be:
\[\sqrt {{{(2\sqrt 2 )}^2} + {{(2\sqrt 2 )}^2}} \\
\Rightarrow \sqrt {8 + 8} \\
\Rightarrow \sqrt {16} \\
\therefore 4m\]

Hence, option A is the correct answer.

Note:Center of mass can only change its position when there is some force applied to it. In case of change of center of mass, only the initial and the final position is considered. But, the individual center of mass depends on the magnitude and direction of the force applied.