Question

The mass of a simple pendulum bob is $ 100gm $ . The length of the pendulum is $ 1m $ . The bob is drawn aside from the equilibrium position so that the string makes an angle of $ {60^ \circ } $ with the vertical and let go. The kinetic energy of the bob while crossing its equilibrium position will be:
 $ \left( A \right){\text{ 0}}{\text{.49J}} $
 $ \left( B \right){\text{ 0}}{\text{.94J}} $
 $ \left( C \right){\text{ 1J}} $
 $ \left( D \right){\text{ 1}}{\text{.2J}} $

Answer 1

Hint: Here in this question the concept of kinetic energy and the potential energy will be needed and for this, we have the relation which is given by, kinetic energy at $ A $ will be equal to change in potential energy between $ A\& B $ . And by solving it we will get the result.

Formula used:
Potential energy,
 $ P = mgh $
Here, $ P $ will be the potential energy
 $ m $ , will be the mass
 $ g $ , will be the gravitational constant
 $ h $ , will be the height
Kinetic energy,
 $ K = \dfrac{1}{2}m{v^2} $
Here, $ v $ will be the velocity.

Complete step by step solution:
So in the question, we have the masses of two bob given and the angle between the string is also given to us which is $ {60^ \circ } $ . So there will be the gap made between the two pendulums as a height and it will be denoted by $ h $

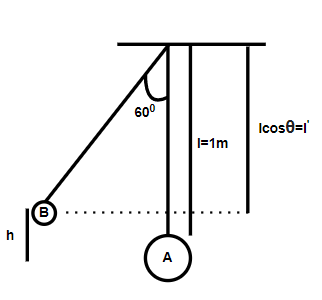
So from the figure, $ h = l - l' $
And as we know $ l' = l\cos \theta $ , so on substituting the values, we will get
 $ \Rightarrow h = l - l\cos {60^ \circ } $
And solving it we will get $ h = \dfrac{1}{2} $
Since the kinetic energy at position $ B $ is zero and the potential energy at this position will be equal to $ mgh $
So by using the law of conservation of energy, we will get the equation as
 $ \Rightarrow mgh + 0 = 0 + K.{E_A} $
So from here, kinetic energy $ A $ will be
 $ \Rightarrow K.{E_A} = mgh $
Now on substituting the values, we will get the equation as
 $ \Rightarrow K.{E_A} = \dfrac{{100}}{{1000}} \times 9.8 \times \dfrac{1}{2} $
And on solving it we will get
 $ \Rightarrow K.{E_A} = 0.49J $
Therefore, the kinetic energy will be equal to $ 0.49J $
Hence, the option $ \left( A \right) $ is correct.

Note:
While solving this we should not forget to have a look at the units as we can see that the unit given is in gram so we have to change it first to get the correct values. And also mentioning the unit in the solution should be the top-most priority.