Question

The magnitude of electric force on a 2$\mu c$ charge placed at the centre o of two equilateral triangle each of side 10 cm, as shown in the figure is P. If charge A,B,C,D,E & F are 2$\mu c$, 2$\mu c$, 2$\mu c$, -2$\mu c$, -2$\mu c$, -2$\mu c$ respectively, then P is:

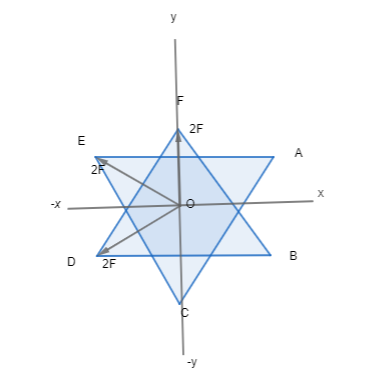
A.21.6 N
B.64.8 N
C.0
D.43.2 N

Answer 1

Hint: Study the electrostatic force and how the charges behave. First find out the force due to every individual force then take their vector sum to find out the total force.
Formula used:

$F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{1}}{{q}_{2}}}{{{r}^{2}}}$

Complete step by step answer:
The superposition of electrostatic force can be defined as if there are a number of charges interacting, the force between two charges is not affected by other charges present. The total force on a charge will be due to the vector sum of the forces due to all the charges individually.

Electrostatic force between two charges ${{q}_{1}}\And {{q}_{2}}$ at a distance r is given by,
$F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{1}}{{q}_{2}}}{{{r}^{2}}}$

Where, ${{\varepsilon }_{0}}$ is the permittivity of free space

$\dfrac{1}{4\pi {{\varepsilon }_{0}}}=8.98\times {{10}^{9}}N{{m}^{2}}{{C}^{-2}}\approx 9\times {{10}^{9}}N{{m}^{2}}{{C}^{-2}}$

Now, it is given that

${{q}_{0}}=2\mu C,{{q}_{A}}=2\mu C,{{q}_{B}}=2\mu C,{{q}_{c}}=2\mu C,{{q}_{D}}=-2\mu C,{{q}_{E}}=-2\mu C,{{q}_{F}}=-2\mu C$

Again, the triangle is an equilateral triangle with side. Its centre will be same as the incentre,
So, the distance from any one of the vertices to the centre is the same as the radius of the circumcircle.
So,

$\begin{align}
  & OA=\dfrac{l}{\sqrt{3}} \\
 & OA=\dfrac{10cm}{\sqrt{3}}=5.77cm \\
\end{align}$

It will be the same for all the vertices to the centre distance.

Now applying the Coulomb’s law for each pair of charges,

$\begin{align}
  & F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{1}}{{q}_{2}}}{{{r}^{2}}} \\
 & {{F}_{AO}}=9\times {{10}^{9}}\times \dfrac{2\mu C\times 2\mu C}{{{\left( 5.77 \right)}^{2}}}=10.81N \\
 & {{F}_{BO}}=9\times {{10}^{9}}\times \dfrac{2\mu C\times 2\mu C}{{{\left( 5.77 \right)}^{2}}}=10.81N \\
 & {{F}_{CO}}=9\times {{10}^{9}}\times \dfrac{2\mu C\times 2\mu C}{{{\left( 5.77 \right)}^{2}}}=10.81N \\
 & {{F}_{DO}}=9\times {{10}^{9}}\times \dfrac{-2\mu C\times 2\mu C}{{{\left( 5.77 \right)}^{2}}}=-10.81N \\
 & {{F}_{EO}}=9\times {{10}^{9}}\times \dfrac{-2\mu C\times 2\mu C}{{{\left( 5.77 \right)}^{2}}}=-10.81N \\
 & {{F}_{FO}}=9\times {{10}^{9}}\times \dfrac{-2\mu C\times 2\mu C}{{{\left( 5.77 \right)}^{2}}}=-10.81N \\
\end{align}$

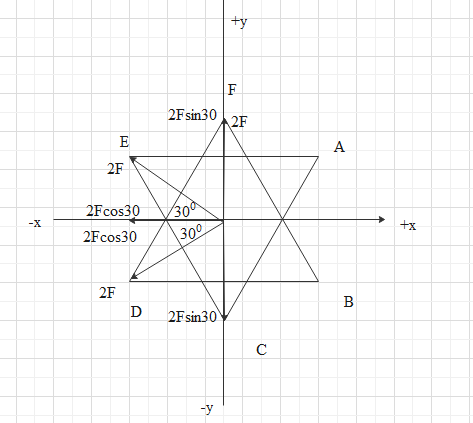
Due to the attraction of opposite charge and deflection of same charge, Force on O due to A is along OD, Force on O due to B is along OE, Force on O due to C is along OF, Force on O due to D is along OD, Force on O due to E is along OE, Force on O due to F is along OF.

So, we have along OD 2F N, along OE 2F N and along OF 2N force.

Breaking them into components,

Along negative y direction we have $2F\sin 30$
Along negative x direction we have $4F\cos 30$
Along positive y direction we have $2F+2F\sin 30$

Reducing the data,

Along negative x direction we have $4F\cos 30$
Along positive y direction we have $2F$

Total force is

 $\begin{align}
  & {{F}_{T}}=-4F\cos 30\hat{i}+2F\hat{j} \\
 & {{F}_{T}}=-4\times 10.81\times 0.866\hat{i}+2\times 10.81\hat{j} \\
 & {{F}_{T}}=-37.44\hat{i}+21.62\hat{j} \\
\end{align}$

Taking magnitude,

$\begin{align}
  & {{F}_{T}}=\sqrt{{{37.44}^{2}}+{{21.62}^{2}}} \\
 & {{F}_{T}}=43.2N \\
\end{align}$

The force on the charge on the centre is 43.2 N

The correct option is (D)

Note: In this type of numerical find out the forces due to individual charge. The break the forces into their components taking suitable co-ordinates. Then we can easily find the total force in any charge in a group of charges.