Question

The magnetic field due to a square loop of side $a$ carrying a current $I$ at its centre is:
$A. \dfrac{\mu_{0}i}{2a}$
$B. \dfrac{\mu_{0}i}{\sqrt 2\pi a}$
$C. \dfrac{\mu_{0}i}{2\pi a}$
$D. \sqrt 2 \dfrac{\mu_{0}i}{\pi a}$

Answer 1

Hint: We know that an electricity and magnetism are inter connected. We also know that the current carrying conductor produces magnetic field in its surrounding and similarly, a changing magnetic field induces current in the coil.
Formula used:
$B=\dfrac{\mu_{0}i}{4\pi r}$

Complete answer:
We know that the magnetic field is an invisible vector force which influences an electric charge and a few magnetic metals. Since it’s a vector clearly, it has both direction and magnitude. A magnet has two different poles, namely the North and the South Pole .Generally, the like poles attract, while the unlike poles repel. This is saying that, North Pole of one magnet repels from the north pole of another magnet, this is true for two South Pole also. However, if a North Pole of one magnet is brought near the south pole of another magnet, then they attract.
We also know from ampere's law that the magnetic field is produced due to a current that is independent of time. We also know that the ampere’s circuital law is the line integral of the magnetic field is equal to the sum of the current in the closed loop, given as
$\mu_{0}I=\oint{\vec{B}.d\vec{l}}$
From this we also know that the magnetic field $B$ for a straight wire is given as, $B=\dfrac{\mu_{0}i}{4\pi r}$
Clearly, from the right hand thumb rule, since the magnetic field inside the loop is directed into the paper, we can say that the net magnetic field at P is the sum total of all the magnetic fields due to the current carrying loop. Consider the square as shown below:

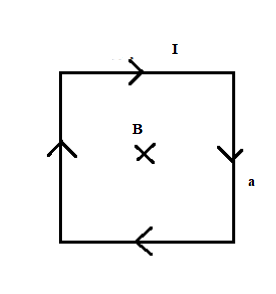
We can consider the square to be made up of 4 straight current carrying conductors, then we have, $B=4\times \dfrac{\mu_{0}i}{4\pi r}$
Substituting the values, we get,
$\implies B= 4\times \dfrac{\mu_{0}I}{4\pi a}$
$\therefore B= \dfrac{\mu_{0}I}{\pi a}$

Thus the correct answer is option $A. \dfrac{\mu_{0}i}{2a}$

Note:
We know that the magnetic field is a vector quality, and hence has both direction and magnitude. We can also say that, the direction of the magnetic field is given from the right hand thumb rule, provided, the direction of the current is known. And vice-versa.