Question

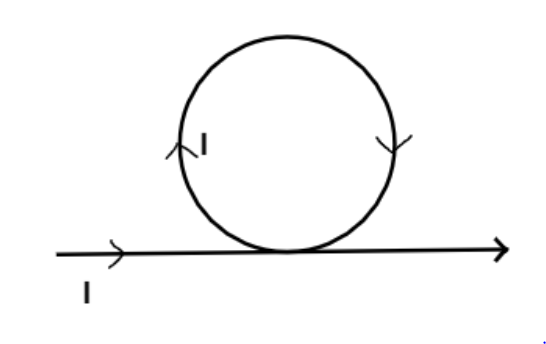
The magnetic field at the center loop in the circuit carrying current I shown in figure is:

$
  (a){\text{ }}\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2I}}{r}\left( {1 + \pi } \right) \\
  (b){\text{ }}\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2I}}{r}\left( {\pi - 1} \right) \\
  (c){\text{ }}\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2I}}{r} \\
  (d){\text{ }}\dfrac{{{\mu _0}}}{{4\pi }}\dfrac{I}{r}\left( {1 + \pi } \right) \\
$

Answer 1

Hint: In the figure there are two current carrying elements that are the circular loop and the finite wire. Use the direct formula for magnetic field at a distance r for a circular loop and finite wire. Then find the net magnetic field at the center. This will help getting the right option.

Complete Step-by-Step solution:
 As we know for an finitely long wire the magnetic field (${B_1}$) is given as
${B_1} = \dfrac{{{\mu _0}I}}{{2\pi r}}$ $wb/{m^2}$, where r is the perpendicular length from the center of the circle as we have to calculate the magnetic field at the center of the circle which is nothing but the radius of the circle as line is touching to the circle.
And for a circular loop the magnetic field (${B_2}$) is given as
${B_2} = \dfrac{{{\mu _0}I}}{{2r}}$$wb/{m^2}$, where r is the radius of the circular loop.
So the net magnetic field (B) of their combination is the difference of respective magnetic fields.
As we see that ${B_2}$ is greater than ${B_1}$ as the denominator of ${B_1}$ is larger than the denominator of ${B_2}$therefore net magnetic field is
$ \Rightarrow B = {B_2} - {B_1}$
Now substitute the values we have,
$ \Rightarrow B = \dfrac{{{\mu _0}I}}{{2r}} - \dfrac{{{\mu _0}I}}{{2\pi r}}$
Now take $\dfrac{{{\mu _0}I}}{{2\pi r}}$ as common we have,
$ \Rightarrow B = \dfrac{{{\mu _0}I}}{{2\pi r}}\left( {\pi - 1} \right)$ $wb/{m^2}$
This expression is also written as
$ \Rightarrow B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2I}}{r}\left( {\pi - 1} \right)$ $wb/{m^2}$
So this is the required answer.
Hence option (B) is the correct answer.

Note – It is always advisable to understand the geometry of the figure while solving problems of this kind as it helps knowing out the basic figures from which current is flowing. Current always leads to production of magnetic fields. The direct formula for magnetic fields due to basic figures need to be remembered, some of them are being mentioned above.