Question

The lower window of a house is at a height of 2 m above the ground and its upper window is 4 m vertically above the lower window. At a certain instant the angle of elevation of the balloon from these windows are observed to be \[{{60}^{\circ }}\] and \[{{30}^{\circ }}\] respectively. Then the height of the balloon above ground is:
A. 12 meters
B. 14 meters
C. 8 meters
D. 16 meters

Answer 1

Hint: Draw the rough diagram according to the figure. It forms 2 triangles. Thus consider both the triangles and by basic trigonometric properties, solve the expression obtained. Then find the total height of the balloon from the ground.

Complete step-by-step answer:

Consider GL as the ground level window 1 as \[{{W}_{1}}\] and window 2 as \[{{W}_{2}}\].

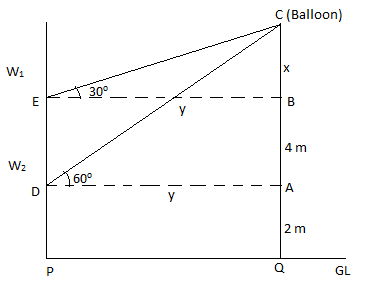
The lower window, \[{{W}_{1}}\] is 2 m from the ground level. The window, \[{{W}_{2}}\] is 4 m above \[{{W}_{1}}\], which means that \[{{W}_{2}}\] is at a height of 6 m from the ground level.

Let the ground level GL be PQ. From the figure we can say that PQ is parallel to AD and PQ is parallel to BE.

Thus \[PQ||AD\] and \[PQ||BE\].

So we can say that PQ = AD and PQ = BE.

\[\therefore AD=BE\]

Let us consider that AD = BE = y.

C is the position of the balloon.

First let us consider \[\Delta BEC\].

\[\tan {{30}^{\circ }}=\dfrac{Opposite\text{ }side}{Adjacent\text{ }side}=\dfrac{BC}{BE}\]

We know from the trigonometric table that, \[\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}\].

Let us consider BC as x.

\[\therefore \tan {{30}^{\circ }}=\dfrac{BC}{BE}\]

\[\Rightarrow \dfrac{x}{y}=\dfrac{1}{\sqrt{3}}\]

Cross multiply the above expression.

\[y=x\sqrt{3}.......(1)\]

Now let us consider \[\Delta ADC\].

\[\tan {{60}^{\circ }}=\dfrac{Opposite\text{ }side}{Adjacent\text{ }side}=\dfrac{AC}{AD}\]

From the trigonometric table, we know that \[\tan {{60}^{\circ }}=\sqrt{3}\].

From figure, AC = AB + BC = 4 + x.

\[\sqrt{3}=\dfrac{4+x}{y}\]

Cross multiply the expression.

\[y=\dfrac{4+x}{3}.......(2)\]

Now let us equate both equation (1) and (2) and get the value of x.

\[\begin{align}

  & x\sqrt{3}=\dfrac{4+x}{\sqrt{3}} \\

 & \Rightarrow x\sqrt{3}.\sqrt{3}=4+x \\

\end{align}\]

\[\begin{align}

  & 3x=4+x \\

 & 2x=4 \\

 & \Rightarrow x={}^{4}/{}_{2}=2 \\

\end{align}\]

Thus we got x = 2, i.e. length of BC = 2 m.

Now we need to find the height of the balloon from ground level.

\[CQ=QA+AB+BC=2+4+2=8m\] [From the figure]

\[\therefore \]The height of the balloon from the ground is \[8m\].

Option C is the correct answer.

Note: We have used basic trigonometric identities, thus you should remember the trigonometric table to solve the same. After finding the value of x, remember to add to find the total height of the balloon from the ground.