
The locus of point of intersection of tangents to the parabolas ${{y}^{2}}=4(x+1)$ and ${{y}^{2}}=8(x+2)$ which are perpendicular to each other is
(a) $x+7=0$
(b) $x-y=4$
(c) $x+3=0$
(d) $y-x=12$
Answer
602.7k+ views
Hint: The general equation of the tangent of a parabola is $y=mx+\dfrac{a}{m}$. Write the general equations of the tangents, for both the parabola separately, and then evaluate the product of their slopes to be equal to -1, since it is given that the tangents are perpendicular to each other.
Complete step-by-step solution -
Let the equation of parabola P1 be ${{y}^{2}}=4(x+1)$ and that of parabola P2 be ${{y}^{2}}=8(x+2)$.
Working on P1 first, we know that its equation is ${{y}^{2}}=4(x+1)$. To make it a bit similar to the general form of a parabola, which is ${{y}^{2}}=4ax$, we’ll have to shift the origin to do away with the constant term in P1.
Shifting the origin is done by assuming new variables $(X,Y)$ in place of old variables $(x,y)$ such that there is some relation between them.
To bring P1 closer to the general form, we need to eliminate the constant term, which is there with $x$. Thus, for new variables $(X,Y)$, our relations would be : $\begin{align}
& X=x+1 \\
& Y=y \\
\end{align}$
Replacing these variables in the equation of P1, we have the new equation as :
${{Y}^{2}}=4X$. Now, this equation can be easily compared with the general equation ${{y}^{2}}=4ax$. On comparing, we find that for P1, $\begin{align}
& 4a=4 \\
& \Rightarrow a=1 \\
\end{align}$
We can now write the equation of a general tangent to P1, since we have the value of $a$, and in the equation $m$ is the slope variable. The equation of tangent to a parabola ${{y}^{2}}=4ax$, is : $y=mx+\dfrac{a}{m}$, where $m$ is variable.
Likewise, for P1, the equation of tangent will be : $\begin{align}
& Y=mX+\dfrac{a}{m} \\
& \Rightarrow Y=mX+\dfrac{1}{m} \\
\end{align}$
Now that we have the equation of the tangent, let’s go back to our original coordinate system (the one before shifting) and replace $X$ and $Y$.
Substituting for $X$ and $Y$, we get :
$\begin{align}
& Y=mX+\dfrac{1}{m} \\
& \Rightarrow y=m(x+1)+\dfrac{1}{m} \\
& \Rightarrow y=mx+m+\dfrac{1}{m} \\
\end{align}$
Let’s call the equation of tangent to P1 in terms of $x$ and $y$ as equation (1).
Now coming to parabola P2, the equation we have is ${{y}^{2}}=8(x+2)$.
We’ll again have to perform shifting of origin to compare it with the general form of a parabola.
To shift the origin for this parabola, we again define new parameters $(X1,Y1)$ and replace $(x,y)$ with them based on a relation.
We have to do away with the constant term here as well, so the new relations would be :
$\begin{align}
& X1=x+2 \\
& Y1=y \\
\end{align}$
Hence, replacing $(x,y)$ in P2, we get : $Y{{1}^{2}}=8X1$
Comparing it to the general form of a parabola, we have :
$\begin{align}
& 4a=8 \\
& \Rightarrow a=2 \\
\end{align}$
We can now write the equation of general tangent to this parabola as well. Let the slope variable be $p$ here. The equation of common tangent to this parabola would be : $\begin{align}
& Y1=pX1+\dfrac{a}{p} \\
& \Rightarrow Y1=pX1+\dfrac{2}{p} \\
\end{align}$ …………………(2)
It is given in the question that these two tangents have to be perpendicular. Therefore, the product of their slopes = -1
Or, $\begin{align}
& pm=-1 \\
& \Rightarrow p=-\dfrac{1}{m} \\
\end{align}$
Replacing $p$ in (2), we get :
$\begin{align}
& Y1=pX1+\dfrac{2}{p} \\
& \Rightarrow Y1=-\dfrac{X1}{m}-2m \\
\end{align}$
Now, let’s go back to the original coordinate system. To do so, we have to replace $X1$ and $Y1$ with their values in terms of $x$ and $y$ respectively.
$\begin{align}
& Y1=-\dfrac{X1}{m}-2m \\
& \Rightarrow y=-\dfrac{x+2}{m}-2m \\
& \Rightarrow -y=\dfrac{x+2+2{{m}^{2}}}{m} \\
\end{align}$ ………………………(3)
Since we need to find the locus of the point of these tangents’ intersection, let’s assume the coordinates of the point as $(h,k)$.
Since this is an intersection point, $(h,k)$ will satisfy the equations of both the tangents. Therefore, substituting for this point in (2) and (3), we get :
$\begin{align}
& y=mx+m+\dfrac{1}{m} \\
& \Rightarrow k=mh+m+\dfrac{1}{m} \\
& \Rightarrow k=\dfrac{{{m}^{2}}h+{{m}^{2}}+1}{m} \\
& \Rightarrow mk={{m}^{2}}h+{{m}^{2}}+1 \\
& \Rightarrow {{m}^{2}}(h+1)-mk+1=0 \\
\end{align}$ and $\begin{align}
& -y=\dfrac{x+2+2{{m}^{2}}}{m} \\
& \Rightarrow -k=\dfrac{h+2+2{{m}^{2}}}{m} \\
& \Rightarrow -mk=h+2+2{{m}^{2}} \\
& \Rightarrow 2{{m}^{2}}+mk+(h+2)=0 \\
\end{align}$
Hence, we have two quadratic equations in $m$. These two equations should ultimately make us reach the same values for $m$, and hence we can compare the coefficients of these two equations.
Doing so, we’ll have :
$\begin{align}
& \dfrac{h+1}{2}=-\dfrac{k}{k}=\dfrac{1}{h+2} \\
& \Rightarrow \dfrac{h+1}{2}=-1=\dfrac{1}{h+2} \\
& \Rightarrow h+1=-2 \\
& \Rightarrow h+3=0 \\
& or,\dfrac{1}{h+2}=-1 \\
& \Rightarrow h+2=-1 \\
& \Rightarrow h+3=0 \\
\end{align}$
Therefore, we have an equation for the $x$ coordinate of the point of intersection. To make this equation look like a locus, all we have to do is replace $(h,k)$ with $(x,y)$. Doing so, we get :
$\begin{align}
& h+3=0 \\
& \Rightarrow x+3=0 \\
\end{align}$ and this is the required locus.
Hence, our required locus is option (c) $x+3=0$
Note: Be very careful while shifting the origin. Shifting the origin is only a temporary process, and we use it only to make comparisons with the general form easier.
In the part where we compare the quadratic equations for m, the theory can be interpreted like, if there are two quadratic equations in $x$, then for them to values that satisfy both the equations, it is absolutely necessary that one equation is nothing but the other equation multiplied by a scalar. This scalar is what we find out by taking the ratio of the coefficients of each term, and only then do we find values of $x$ satisfying both the equations.
Here’s a drawing to illustrate the result of this question :
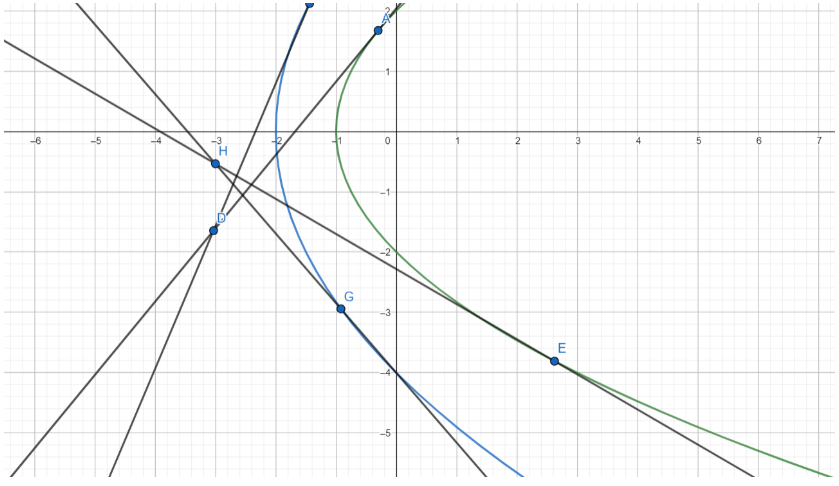
Here, we can see two points $H$ and $D$ which are the intersection points of tangents to the two parabolas, and both of them lie on the line $x+3=0$.
Complete step-by-step solution -
Let the equation of parabola P1 be ${{y}^{2}}=4(x+1)$ and that of parabola P2 be ${{y}^{2}}=8(x+2)$.
Working on P1 first, we know that its equation is ${{y}^{2}}=4(x+1)$. To make it a bit similar to the general form of a parabola, which is ${{y}^{2}}=4ax$, we’ll have to shift the origin to do away with the constant term in P1.
Shifting the origin is done by assuming new variables $(X,Y)$ in place of old variables $(x,y)$ such that there is some relation between them.
To bring P1 closer to the general form, we need to eliminate the constant term, which is there with $x$. Thus, for new variables $(X,Y)$, our relations would be : $\begin{align}
& X=x+1 \\
& Y=y \\
\end{align}$
Replacing these variables in the equation of P1, we have the new equation as :
${{Y}^{2}}=4X$. Now, this equation can be easily compared with the general equation ${{y}^{2}}=4ax$. On comparing, we find that for P1, $\begin{align}
& 4a=4 \\
& \Rightarrow a=1 \\
\end{align}$
We can now write the equation of a general tangent to P1, since we have the value of $a$, and in the equation $m$ is the slope variable. The equation of tangent to a parabola ${{y}^{2}}=4ax$, is : $y=mx+\dfrac{a}{m}$, where $m$ is variable.
Likewise, for P1, the equation of tangent will be : $\begin{align}
& Y=mX+\dfrac{a}{m} \\
& \Rightarrow Y=mX+\dfrac{1}{m} \\
\end{align}$
Now that we have the equation of the tangent, let’s go back to our original coordinate system (the one before shifting) and replace $X$ and $Y$.
Substituting for $X$ and $Y$, we get :
$\begin{align}
& Y=mX+\dfrac{1}{m} \\
& \Rightarrow y=m(x+1)+\dfrac{1}{m} \\
& \Rightarrow y=mx+m+\dfrac{1}{m} \\
\end{align}$
Let’s call the equation of tangent to P1 in terms of $x$ and $y$ as equation (1).
Now coming to parabola P2, the equation we have is ${{y}^{2}}=8(x+2)$.
We’ll again have to perform shifting of origin to compare it with the general form of a parabola.
To shift the origin for this parabola, we again define new parameters $(X1,Y1)$ and replace $(x,y)$ with them based on a relation.
We have to do away with the constant term here as well, so the new relations would be :
$\begin{align}
& X1=x+2 \\
& Y1=y \\
\end{align}$
Hence, replacing $(x,y)$ in P2, we get : $Y{{1}^{2}}=8X1$
Comparing it to the general form of a parabola, we have :
$\begin{align}
& 4a=8 \\
& \Rightarrow a=2 \\
\end{align}$
We can now write the equation of general tangent to this parabola as well. Let the slope variable be $p$ here. The equation of common tangent to this parabola would be : $\begin{align}
& Y1=pX1+\dfrac{a}{p} \\
& \Rightarrow Y1=pX1+\dfrac{2}{p} \\
\end{align}$ …………………(2)
It is given in the question that these two tangents have to be perpendicular. Therefore, the product of their slopes = -1
Or, $\begin{align}
& pm=-1 \\
& \Rightarrow p=-\dfrac{1}{m} \\
\end{align}$
Replacing $p$ in (2), we get :
$\begin{align}
& Y1=pX1+\dfrac{2}{p} \\
& \Rightarrow Y1=-\dfrac{X1}{m}-2m \\
\end{align}$
Now, let’s go back to the original coordinate system. To do so, we have to replace $X1$ and $Y1$ with their values in terms of $x$ and $y$ respectively.
$\begin{align}
& Y1=-\dfrac{X1}{m}-2m \\
& \Rightarrow y=-\dfrac{x+2}{m}-2m \\
& \Rightarrow -y=\dfrac{x+2+2{{m}^{2}}}{m} \\
\end{align}$ ………………………(3)
Since we need to find the locus of the point of these tangents’ intersection, let’s assume the coordinates of the point as $(h,k)$.
Since this is an intersection point, $(h,k)$ will satisfy the equations of both the tangents. Therefore, substituting for this point in (2) and (3), we get :
$\begin{align}
& y=mx+m+\dfrac{1}{m} \\
& \Rightarrow k=mh+m+\dfrac{1}{m} \\
& \Rightarrow k=\dfrac{{{m}^{2}}h+{{m}^{2}}+1}{m} \\
& \Rightarrow mk={{m}^{2}}h+{{m}^{2}}+1 \\
& \Rightarrow {{m}^{2}}(h+1)-mk+1=0 \\
\end{align}$ and $\begin{align}
& -y=\dfrac{x+2+2{{m}^{2}}}{m} \\
& \Rightarrow -k=\dfrac{h+2+2{{m}^{2}}}{m} \\
& \Rightarrow -mk=h+2+2{{m}^{2}} \\
& \Rightarrow 2{{m}^{2}}+mk+(h+2)=0 \\
\end{align}$
Hence, we have two quadratic equations in $m$. These two equations should ultimately make us reach the same values for $m$, and hence we can compare the coefficients of these two equations.
Doing so, we’ll have :
$\begin{align}
& \dfrac{h+1}{2}=-\dfrac{k}{k}=\dfrac{1}{h+2} \\
& \Rightarrow \dfrac{h+1}{2}=-1=\dfrac{1}{h+2} \\
& \Rightarrow h+1=-2 \\
& \Rightarrow h+3=0 \\
& or,\dfrac{1}{h+2}=-1 \\
& \Rightarrow h+2=-1 \\
& \Rightarrow h+3=0 \\
\end{align}$
Therefore, we have an equation for the $x$ coordinate of the point of intersection. To make this equation look like a locus, all we have to do is replace $(h,k)$ with $(x,y)$. Doing so, we get :
$\begin{align}
& h+3=0 \\
& \Rightarrow x+3=0 \\
\end{align}$ and this is the required locus.
Hence, our required locus is option (c) $x+3=0$
Note: Be very careful while shifting the origin. Shifting the origin is only a temporary process, and we use it only to make comparisons with the general form easier.
In the part where we compare the quadratic equations for m, the theory can be interpreted like, if there are two quadratic equations in $x$, then for them to values that satisfy both the equations, it is absolutely necessary that one equation is nothing but the other equation multiplied by a scalar. This scalar is what we find out by taking the ratio of the coefficients of each term, and only then do we find values of $x$ satisfying both the equations.
Here’s a drawing to illustrate the result of this question :

Here, we can see two points $H$ and $D$ which are the intersection points of tangents to the two parabolas, and both of them lie on the line $x+3=0$.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




