
The line \[x - 7 = 0\] is
A.Parallel to \[y\]-axis.
B.Parallel to \[x\]-axis.
C.Passing through the origin.
D.None of these.
Answer
553.2k+ views
Hint: We will first solve the given equation to find the value of \[x\]. We will then form a table to find the value of \[x\] with respect to \[y\]. We will then draw a graph using the table to find the nature of the line whether it is parallel to \[x\]-axis, \[y\]-axis or passing through the origin.
Complete step by step solution:
We will first solve the given equation to find the value of \[x\]. We will then form a table to find the value of \[x\] with respect to \[y\]. We will then draw a graph using the table to find the nature of the line whether it is parallel to \[x\]-axis, \[y\]-axis or passing through the origin.
Hence, from this table it is proved that for any value of \[y\] (both negative and positive), \[x\] will always hold the same value.
Hence, the graph of the line \[x - 7 = 0\] will be:
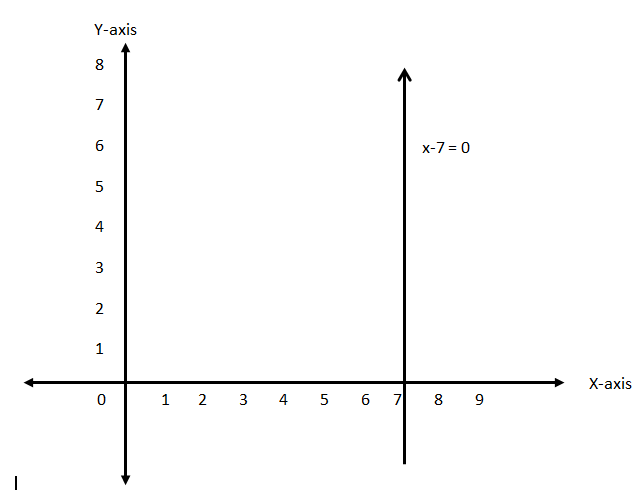
From this graph, we can say that it holds a constant value of \[x = 7\] and it is parallel to \[y\]-axis.
Hence, option A is the correct option.
Note: Since, the line is parallel to \[y\]-axis, clearly, it should be perpendicular to \[x\]-axis. Also, from the graph, the line makes a right angle with \[x\]-axis hence, it is perpendicular to it. The equation of a straight line parallel to \[y\]-axis at a distance ‘\[a\]’ from it is \[x = a\].
Also, the equation of a straight line parallel to \[x\]-axis at a distance ‘b’ from it is \[y = b\]. The equation of \[y\]-axis is \[x = 0\] , because \[y\]-axis is parallel to itself at a distance 0 from it. Similarly, the equation of \[x\]-axis is \[y = 0\] , because \[x\]-axis is parallel to itself at a distance 0 from it.
Complete step by step solution:
We will first solve the given equation to find the value of \[x\]. We will then form a table to find the value of \[x\] with respect to \[y\]. We will then draw a graph using the table to find the nature of the line whether it is parallel to \[x\]-axis, \[y\]-axis or passing through the origin.
| \[x\] | 7 | 7 | 7 | 7 | 7 | 7 |
| \[y\] | \[ - 2\] | \[ - 1\] | 0 | 1 | 2 | 3 |
Hence, from this table it is proved that for any value of \[y\] (both negative and positive), \[x\] will always hold the same value.
Hence, the graph of the line \[x - 7 = 0\] will be:

From this graph, we can say that it holds a constant value of \[x = 7\] and it is parallel to \[y\]-axis.
Hence, option A is the correct option.
Note: Since, the line is parallel to \[y\]-axis, clearly, it should be perpendicular to \[x\]-axis. Also, from the graph, the line makes a right angle with \[x\]-axis hence, it is perpendicular to it. The equation of a straight line parallel to \[y\]-axis at a distance ‘\[a\]’ from it is \[x = a\].
Also, the equation of a straight line parallel to \[x\]-axis at a distance ‘b’ from it is \[y = b\]. The equation of \[y\]-axis is \[x = 0\] , because \[y\]-axis is parallel to itself at a distance 0 from it. Similarly, the equation of \[x\]-axis is \[y = 0\] , because \[x\]-axis is parallel to itself at a distance 0 from it.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

Which animal has three hearts class 11 biology CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




