
The line segment joining the points (3, -4) and (1,2) is trisected at the points P and Q. If the coordinates of P and Q are (p, -2) and ( $\dfrac{5}{3}$, q) respectively, find the values of p and q.
A. p = $\dfrac{7}{3}$, q = – 3
B. p = $\dfrac{7}{3}$, q = 0
C. p = $\dfrac{5}{3}$, q = 0
D. None of these
Answer
600.3k+ views
Hint: In this question to find the values of p and q, we will use the section formula and then check each given option to find out which are correct.
Complete step-by-step answer:
Now, we will use the section formula. The section formula tells us the coordinates of a point which divides a given line segment into two parts such that their lengths are in the ratio m: n. The Section formula to find a point (x, y) is
x = $\dfrac{{{\text{m}}{{\text{x}}_2}{\text{ + n}}{{\text{x}}_1}}}{{{\text{m + n}}}}$
y = $\dfrac{{{\text{m}}{{\text{y}}_2}{\text{ + n}}{{\text{y}}_1}}}{{{\text{m + n}}}}$
Here we are given two points. Let's say A (3, -4) and B (1,2) make a line segment AB. The line segment AB is trisected at points P and Q. So, we will apply section formula both at point P and Q. As, P divides line segment AB in ratio 1:2.
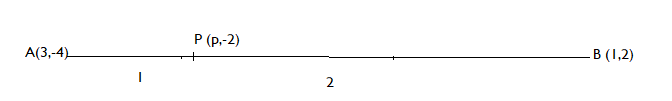
So, applying section formula at point P (p, -2), we get
x – coordinate of P = $\dfrac{{1(1){\text{ + 2(3)}}}}{3}$ = $\dfrac{7}{3}$
$ \Rightarrow $ p = $\dfrac{7}{3}$
As, Q divides the line segment AB in the ratio 2:1.
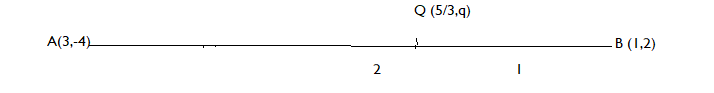
Applying section formula at point Q ( $\dfrac{5}{3}$, q), we get
y – coordinate of Q = $\dfrac{{2(2){\text{ + 1( - 4)}}}}{3}$ = 0
$ \Rightarrow $ q = 0
So, the correct option will be B.
Note: While solving such types of questions, it is important to apply the section formula correctly. Most of the students made a mistake while applying the section formula. They replaced m from n and n from m. Also, apply the proper ratio for finding the coordinates of a point. Also, when only you have to find the value of a given variable, apply only that formula to find the value of the variable, for example if you are given that the x – coordinate of point is k, so you have to apply only the formula to find the x – coordinate of point.
Complete step-by-step answer:
Now, we will use the section formula. The section formula tells us the coordinates of a point which divides a given line segment into two parts such that their lengths are in the ratio m: n. The Section formula to find a point (x, y) is
x = $\dfrac{{{\text{m}}{{\text{x}}_2}{\text{ + n}}{{\text{x}}_1}}}{{{\text{m + n}}}}$
y = $\dfrac{{{\text{m}}{{\text{y}}_2}{\text{ + n}}{{\text{y}}_1}}}{{{\text{m + n}}}}$
Here we are given two points. Let's say A (3, -4) and B (1,2) make a line segment AB. The line segment AB is trisected at points P and Q. So, we will apply section formula both at point P and Q. As, P divides line segment AB in ratio 1:2.
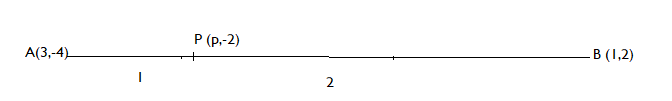
So, applying section formula at point P (p, -2), we get
x – coordinate of P = $\dfrac{{1(1){\text{ + 2(3)}}}}{3}$ = $\dfrac{7}{3}$
$ \Rightarrow $ p = $\dfrac{7}{3}$
As, Q divides the line segment AB in the ratio 2:1.
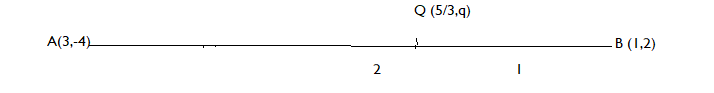
Applying section formula at point Q ( $\dfrac{5}{3}$, q), we get
y – coordinate of Q = $\dfrac{{2(2){\text{ + 1( - 4)}}}}{3}$ = 0
$ \Rightarrow $ q = 0
So, the correct option will be B.
Note: While solving such types of questions, it is important to apply the section formula correctly. Most of the students made a mistake while applying the section formula. They replaced m from n and n from m. Also, apply the proper ratio for finding the coordinates of a point. Also, when only you have to find the value of a given variable, apply only that formula to find the value of the variable, for example if you are given that the x – coordinate of point is k, so you have to apply only the formula to find the x – coordinate of point.
Recently Updated Pages
Master Class 8 Maths: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 7 Maths: Engaging Questions & Answers for Success

Class 7 Question and Answer - Your Ultimate Solutions Guide

Master Class 6 Maths: Engaging Questions & Answers for Success

Class 6 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

Which animal has three hearts class 11 biology CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




